Организация оптимального кольцевого маршрута

МИНИСТЕРСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

«Белорусская государственная академия связи»

ФАКУЛЬТЕТ ИНЖИНИРИНГА И ТЕХНОЛОГИЙ СВЯЗИ

КАФЕДРА ОРГАНИЗАЦИИ И ТЕХНОЛОГИИ ПОЧТОВОЙ СВЯЗИ

Организация оптимального кольцевого маршрута

Пояснительная записка

к курсовой работе

по дисциплине

«ЛОГИСТИКА В ПОЧТОВОЙ СВЯЗИ»

Выполнила студентка гр. ПС 441                                                              К.В. Лаптева

Руководитель  ст. преподаватель                                                     Н.А. Стрельская

Минск 2016

Министерство связи и информатизации Республики Беларусь

Учреждение образования «Белорусская государственная академия связи»

Факультет инжиниринга и технологий связи

Курс _____________________ Шифр________________№КП(КР)_____________

Дисциплина__________________________________________________________

Студент______________________________________________________________

(фамилия, имя, отчество)

Допущен (а) к защите «_______» __________________________ 20____г.

Не допущен (а) к защите «_______» __________________________ 20____г.

Преподаватель ________________________________________________________________

(фамилия, имя, отчество) (подпись)

РЕЦЕНЗИЯ

________________________________________________________________________________
_________________________________________________________________________________
_________________________________________________________________________________
_________________________________________________________________________________
_________________________________________________________________________________
_________________________________________________________________________________
_________________________________________________________________________________
_________________________________________________________________________________
_________________________________________________________________________________
_____________________________________________________
СОДЕРЖАНИЕ

Введение. 4

1 Основные принципы построения почтовой связи на территории Республики Беларусь  8

2 Построение кольцевого маршрута. 10

2.1 Метод ветвей границ. 10

2.2 Метод Дакея. 30

2.3 Метод Дакея-Габра. 32

Заключение. 35

Список использованых источников. 36

Приложение А Схема оптимального кольцевого маршрута. 37

ВВЕДЕНИЕ

Одной из наиболее важных социальных структур, существующей в современном мире, является почта. Современная почтовая сеть предоставляет услуги почтовой связи на всей территории страны, включая все города и сельские населенные пункты. Полный спектр услуг, предоставляемый почтой, стал огромен.

На сегодняшний день РУП «Белпочта» представляет собой единый производственно-технологический комплекс, включающий в себя 6 областных филиалов, филиал «Узел специальной связи», производство «Минская почта» и автотранспортное производство, 117 районных узлов почтовой связи, около 4000 отделений почтовой связи (из них почти 3000-в сельской местности), 11800 доставочных участков и 11200 почтальонов.

Для обеспечения бесперебойной работы почтовой сети в Беларуси функционируют межобластные, межрайонные и внутригородские маршруты по которым курсирует около 1300 автомобилей.

Республиканское унитарное предприятие «Белпочта» выполняет свою главную миссию – предоставление услуг почтовой связи для населения, органов государственного управления, предприятий и организаций, руководствуясь девизом «Быстрота. Надежность. Доступность». За этими тремя словами – строгое соблюдение всех стандартов по приему, обработке, пересылке и доставке всех видов почтовых отправлений, бесперебойное работа техники и транспорта, внедрение и использование новых технологий.

РУП «Белпочта» – крупнейшая организация в стране, которая предоставляет населению услуги по приему различных видов платежей. Важнейшей задачей при этом является сокращение времени обслуживания плательщика, а радикальным решением этой задачи – объединение всех его платежей, подлежащих оплате, в единый лицевой счет. В этом случае платежи проводятся с помощью одной технологической операции. Помимо указанных возможностей, разработанный комплекс позволяет предоставить клиенту дополнительные удобства: выбор конкретного вида платежа, который он желает оплатить, возможность частичной оплаты и авансирования, межрегиональные платежи.

В течение 2015 года проводилась работа по оснащению современными техническими средствами объектов почтовой связи, внедрению новых технологий, развитию услуг почтовой связи, улучшению обслуживания клиентов, в результате чего в РУП «Белпочта» автоматизированы все отделения почтовой связи.

Успешно продолжается сотрудничество РУП «Белпочта» со страховыми компаниями. Развиваются и пользуются популярностью у клиентов РУП «Белпочта» услуги ускоренной почты внутриреспубликанской службы «Экспресс-почта». РУП «Белпочта» продолжает развивать банковские услуги по договорам поручения с различными банками. В настоящее время около 2 тысяч отделений почтовой связи в сельской местности по договору-поручению ОАО «АСБ Беларусбанк» оказывают банковские услуги по вкладным операциям.

Белорусская почта особое внимание уделяет вопросам качества предоставления услуг. В настоящее время РУП «Белпочта» является обладателем международных сертификатов качества:

1.                     Сертификат соответствия системы менеджмента качества СТБ ИСО 9001-2001, зарегистрированный в Государственной системе Республики Беларусь.

2.                     Сертификат в области управления качеством международной почтовой службы Международного Бюро Всемирного почтового союза (ВПС) уровня А («золотого»), полученный 1 мая 2007 года в г. Берне во время сессии Совета почтовой эксплуатации.

3.                     Сертификат Серебряного уровня в программе контроля и оценки качества работы Кооператива EMS по итогам работы 2006 года.

4.                     Сертификат Бронзового уровня в программе контроля и оценки качества Кооператива ЕМS Всемирного почтового союза в 2014 году.

Получение сертификатов является результатом интенсивной и работы персонала РУП «Белпочта» по обеспечению почтовой службы высокого качества.

Таким образом, белорусская почта находится в постоянном развитии, совершенствуя привычные услуги и разрабатывая новые, ежедневно подтверждая свой девиз «Быстрота, надежность, доступность».

В данной курсовой работе будет рассмотрена организация оптимального кольцевого маршрута по данному варианту. Актуальность данной темы обусловлена тем, чтобы сократить до минимума время на перевозку почты и оптимизации почтовых маршрутов. Целью данной курсовой работы является определение оптимального кольцевого маршрута с помощью 3 методов построения.

1 ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ ПОЧТОВОЙ СВЯЗИ       НА       ТЕРРИТОРИИ РЕСПУБЛИКИ БЕЛАРУСЬ

Скорость продвижения почты и письменной корреспонденции, а соответственно, и качество предоставляемых услуг почтовой связи напрямую зависят от организации перевозки. Поэтому перевозка почты – это главная составляющая в едином технологическом процессе по пересылке почтовых отправлений, в котором все производительные процессы связаны между собой элементами перевозки и осуществляются на основании закона «О почтовой связи».

Автотранспорт является одним из основных транспортных средств, который широко используются для перевозки почтовых отправлений и денежных средств. Преимущества этого вида транспорта: гибкость, маневренность, механизация погрузочно-разгрузочных работ, возможность применения его на магистралях, внутриобластных, внутрирайонных, межрайонных, городских и подъездных маршрутах.

По форме построения почтовые авто маршруты подразделяются на: кольцевые, радиальные и комбинированные.

Кольцевым называется маршрут, при котором движение почтового транспорта совершается по замкнутой линии, т.е. по кольцу. Кольцевые маршруты более экономичны, чем радиальные, но, как правило, протяженность их не должна превышать 100 - 120 км, так как при большой протяженности доставка почты может быть замедлена.

Радиальным называется маршрут, при котором транспорт движется по прямой или ломаной, но не замкнутой линии в прямом и обратном направлениях. Его следует применять в тех случаях, когда протяженность маршрута составляет более 100 км.

Комбинированным называется маршрут, когда движение транспорта на одних участках осуществляется радиально, а на других по кольцу.

В зависимости от местных условий могут применяться комбинированные маршруты. Комбинированным называется маршрут, где почтовый транспорт на одних участках движется по радиальному маршруту, а на других участках – по кольцевому маршруту.

В городах применяются централизованная, децентрализованная и комбинированная системы обработки и продвижения почтовых отправлений.

При централизованной системе все почтовые отправления обрабатываются в одном городском объекте почтовой связи, что сокращает количество этапов обработки почты, время прохождения, уменьшаются затраты на перевозку почты в городах.

При децентрализованной системе обработки и продвижения почты в городе создаются два или несколько объектов почтовой связи, каждый из которого обрабатывает все виды почтовых отправлений для определенной части города.

В настоящее время обработка и продвижение почтовых отправлений организуется преимущественно на централизованной системе.

С целью удобства и доступности услуг почтовой связи в городах размещаются в почтовые ящики.

Необходимое количество почтовых ящиков для города в целом определяется по нормативам из расчета 2-3 почтовых ящика на 1 км² жилой территории в зависимости от местных условий и до 2 на 1 км² промышленной и коммунально-складской территории.

В пределах города количество почтовых ящиков на 1 км² территории в зависимости от местных условий может быть различным для отдельных районов.

2 ПОСТРОЕНИЕ КОЛЬЦЕВОГО МАРШРУТА 2.1 Метод ветвей границ

Метод «ветвей и границ является наиболее удобным способом построения оптимального кольцевого маршрута. Метод заключается в том, что все множество допустимых решений задачи разбивается на последовательно-уменьшающиеся подмножества при помощи процедуры ветвления. В результате находится последовательность объезда пунктов (маршрут), протяженность которого меньше любого другого возможного варианта.

Множество «S» (0) состоит из (n-1)! Циклов, которые разбиваются на 2 не пересекающихся множества «S» (ij) и «S» (ij) для которых вычисляются их оценки. Далее подмножества с минимальной оценкой разбивается вновь на 2 не пересекающихся подмножества, и вычисляются их оценки. Это разбиение продолжается до тех пор, пока не получится подмножество, содержащее замкнутый маршрут (цикл) удовлетворяющий наложенным ограничениям.

Этот кольцевой маршрут считается оптимальным. Ограничивающими условиями могут быть минимальный пробег автомашины или минимальные затраты времени на объезд маршрута.

Таблица 2.1.1 - Исходные данные

Пункты начала движения	Пункты конца движения
1	2	3	4	5
1	∞	5	4	5	23
2	8	∞	8	8	5
3	6	8	∞	11	12
4	26	11	11	∞	10
5	14	16	19	16	∞

·                          Выбираем самый минимальный элемент из каждой строки и записываем в графу константа приведения, вычитаем из каждого элемента константу приведения;

 Таблица 2.1.2 - Приведенная матрица (по строкам)

Пункты начала движения	Пункты конца движения	Конст.
1	2	3	4	5
1	∞	5           1	4           0	5        1	23       19	4
2	8          3	∞	8           3	8        3	5          0	5
3	6          0	8           2	∞	11      5	12        6	6
4	26       16	11         1	11         1	∞	10        0	10
5	14        0	16         2	19         5	16      2	∞	14

Таблица 2.1.3 - Приведенная матрица (по столбцам)

Пункты начала движения	Пункты конца движения
1	2	3	4	5
1	∞	1           0	0           0	1           0	19       19
2	3          3	∞	3           3	3           2	0          0
3	0          0	2           1	∞	5           4	6          6
4	16       16	1           0	1           1	∞	0          0
5	0          0	2           1	5           5	2           1	∞
Конст.	0	1	0	1	0

·                        Сумма констант = 41. Так как во всех строках и столбцах есть «0», то рассчитываем для всех нулевых элементов приведенной матрицы значения Q (i и j). Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q (i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца, исключая «0», находящихся в i-строке и в j-столбце.

Q3.1=0+1=1                                    Q1.3=0+1=1

Q5.1=0+1=1                                    Q1.4=1+0=1

Q1.2=0+0=0                                    Q2.5=0+2=2

Q4.2=0+0=0                                    Q4.5=0+0=0

·                          Выбираем наибольшее значение и осуществляем ветвление (множество развивается на 2 непересекающихся множества). Наибольшее значение Q2.5. Столбец и строка данного элемента вычеркивается, в клетке Q5,2 ставится бесконечность и составляется ветвление.

 

                                 43                                                                                                      41

Рисунок 2.1.1 - Начало ветвления дуги 2.5

Рассчитываем нижние границы подмножества.

Нижние границы всех циклов, есть сумма констант приведения.

h 1=4+5+6+10+14+1+1=41              h 1+Q2.5=41+2=43

Далее проводим вторую итерацию:

Так как во всех строках и столбцах есть «0», то константу приведения мы не рассчитываем, а считаем сразу элемент Q (i, j)

Для проведения второй итерации выполняются все те же операции вычисления как при первой итерации.

Таблица 2.1.4 - Приведенная матрица (вторая итерация)

Пункты начала движения	Пункты конца движения
1	2	3	4
1	∞	0	0	0
3	0	1	∞	4
4	16	0	1	∞
5	0	∞	5	1

·                          Сумма констант = 0. Так как во всех строках и столбцах есть «0», то рассчитываем для всех нулевых элементов приведенной матрицы значения Q (i и j). Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q (i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца, исключая «0», находящихся в i-строке и в j-столбце.

Q3.1=0+1=1 (1)                                    Q1.3=0+1=1 (3)

Q5.1=0+1=1 (2)                                    Q1.4=1+0=1 (4)

Q1.2=0+0=0                                           Q4.2=0+1=1 (5)

·                          Получилось 5 возможных вариантов.

Выбираем первое наибольшее значение и осуществляем ветвление. Наибольшее значение Q 3.1. Столбец и строка данного элемента вычеркивается, в клетке Q 1.3 ставится бесконечность и составляется ветвление.

 

                       43                                                             41

                                                               42                        41

 

Рисунок 2.1.2 - Начало ветвления дуги 3.1

Рассчитываем нижние границы подмножества.

h 2=0            h1+h2=41+0=41            h1+h2+Q3.1=41+0+1=42

Таблица 2.1.5 – Приведенная матрица (третья итерация)

Пункты начала движения	Пункты конца движения	Конст.
2	3	4
1	0	∞	0	0
4	0	1	∞	0
5	∞	5  4	1  0	1

·                          Сумма констант = 1. Сделав нули в необходимой строке, рассчитываем для всех нулевых элементов приведенной матрицы значения Q (i и j). Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q (i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца, исключая «0» находящихся в i-строке и в j-столбце.

Q1.3=0+1=1                                   Q4.2=0+1=1

Q5.4=0+4=4                                       Q1.4=0+0=0

Q1.2=0+0=0

Рассчитываем нижние границы подмножества.

h3=1             h1+h2+h3=41+0+1=42            h1+h2+Q5.4=41+0+4=45

         43                                                41

 

      42                                           41

 

          

 

      45

42

Рисунок 2.1.3 - Начало ветвления дуги 5.4

Таблица 2.1.6 - Приведенная матрица (четвёртая итерация)

Пункты начала движения	Пункты конца движения
2	3
1	0	∞
4	0	0

На этом ветвление заканчивается. Включение в варианты дуг Q_4.3 и Q_1.2 образуют дерево.

Полученный вариант: Z (2.5, 3.1, 5.4, 4.3, 1.2)

Затраты времени в первом варианте составили 42 минуты.

 

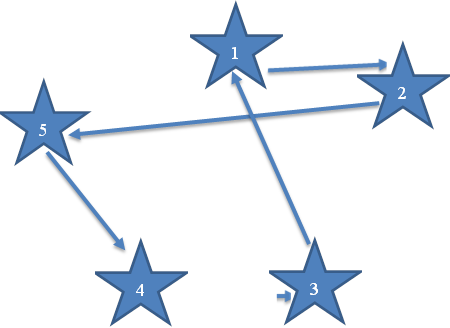Рисунок 2.1.4 – Схема кольцевого маршрута методом ветвей

Выбираем второе наибольшее значение и осуществляем ветвление. Наибольшее значение Q5.1. Столбец и строка данного элемента вычеркивается, в клетке Q1,5 ставится бесконечность и составляется ветвление.

Таблица 2.1.7 - Приведенная матрица (вторая итерация)

Пункты начала движения	Пункты конца движения
1	2	3	4
1	∞	0	0	0
3	0	1	∞	4
4	16	0	1	∞
5	0	∞	5	1

·                          Сумма констант = 0. Так как во всех строках и столбцах есть «0», то рассчитываем для всех нулевых элементов приведенной матрицы значения Q(i и j). Для каждой клетки содержащей «0» записываем значения Q(i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца.

Q3.1=0+1=1 (1)                                    Q1.3=0+1=1 (3)

Q5.1=0+1=1 (2)                                    Q1.4=1+0=1 (4)

Q1.2=0+0=0                                          Q4.2=0+1=1 (5)

 

                                   43                                             41

 

                                                                  42                                           41

Рисунок 2.1.5 - Начало ветвления дуги 5.1

h 2=0     h1+h2=41+0=41            h1+h2+Q5.1=41+0+1=42

Таблица 2.1.8 - Приведенная матрица (третья итерация)

Пункты начала движения	Пункты конца движения
2	3	4	Конст.
1	0	0	0	0
3	1  0	∞	4  3	1
4	0	1	∞	0

·                          Сумма констант = 1. Сделав нули в необходимой строке, рассчитываем для всех нулевых элементов приведенной матрицы значения Q(i и j). Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q(i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца, исключая «0», находящихся в i-строке и в j-столбце.

Q3.2=0+3=3                                   Q4.2=0+1=1                                    

Q1.3=0+1=1                                       Q1.4=0+1=1

Q1.2=0+0=0                                          

Рассчитываем нижние границы подмножества.

h 3=1            h1+h2+h3=41+0+1=42            h1+h2+Q3.2=41+0+3=44

·                          Для каждой клетки содержащей «0» приведенной матрицы записываем значения Q(i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца, исключая «0», находящихся в i-строке и в j-столбце.

                43                                                41

 

                                                      42                                 41

 

44                    42

 

Рисунок 2.1.6 - Начало ветвления дуги 3.2

Таблица 2.1.9 - Приведенная матрица (четвёртая итерация)

Пункты[A1]  начала движения	Пункты конца движения
3	4
1	0	0
4	0	∞

На этом ветвление заканчивается. Включение в варианты дуг Q_4.3 и Q_1.4 образуют дерево.

Полученный вариант: Z (2.5, 5.1, 3.2, 4.3, 1.4)

Затраты времени во втором варианте составили 42 минуты.

 

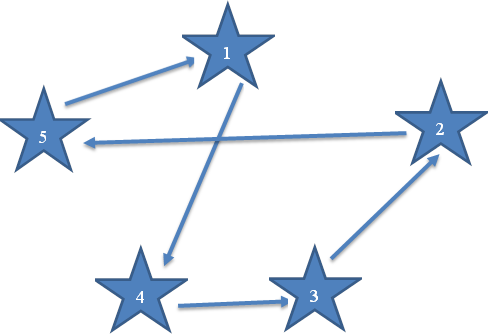
Рисунок 2.1.7 – Схема кольцевого маршрута методом ветвей

Выбираем третье наибольшее значение и осуществляем ветвление. Наибольшее значение Q1.3. Столбец и строка данного элемента вычеркивается, в клетке Q3,1 ставится бесконечность и составляется ветвление.

Таблица 2.1.10 - Приведенная матрица (вторая итерация)

Пункты начала движения	Пункты конца движения
1	2	3	4
1	∞	0	0	0
3	0	1	∞	4
4	16	0	1	∞
5	0	∞	5	1

·                          Сумма констант приведения = 0. Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q(i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца.

Q3.1=0+1=1 (1)                                    Q1.3=0+1=1 (3)

Q5.1=0+1=1 (2)                                    Q1.4=1+0=1 (4)

Q1.2=0+0=0                                          Q4.2=0+1=1 (5)

 

                                      42                                           41

 

                                                                  42                                      41

Рисунок 2.1.8 - Начало ветвления дуги 1.3

Рассчитываем нижние границы подмножества.

h 2=0            h1+h2=41+0=41            h1+h2+Q1.3=41+0+1=42

 Таблица 2.1.11 - Приведенная матрица (третья итерация)

Пункты начала движения	Пункты конца движения
1	2	4	Конст.
3	∞	1    0	4   3  2	1
4	16	0	∞	0
5	0	∞	1  0	0
Конст.	0	0	1

Q3.2=0+2=1                                        Q5.1=0+2=2                                   

Q4.2=0+16=16                                    Q5.4=0+2=2                               

Рассчитываем нижние границы подмножества.

h 3=2     h1+h2+h3=41+0+2=43            h1+h2+Q4.2=41+0+16=57

         43                                           41

42                     41

 

                                      42                       

   57                         43

 

Рисунок 2.1.9 - Начало ветвления дуги 4.2            

Таблица 2.1.12 - Приведенная матрица (четвёртая итерация)

Пункты начала движения	Пункты конца движения
1	4
3	∞	0
5	0	0

На этом ветвление заканчивается. Включение в варианты дуг Q_5.1 и Q_3.4 образуют дерево.

Полученный вариант: Z (2.5, 1.3, 4.2, 5.1, 3.4)

Затраты времени в третьем варианте составили 43 минуты.

 

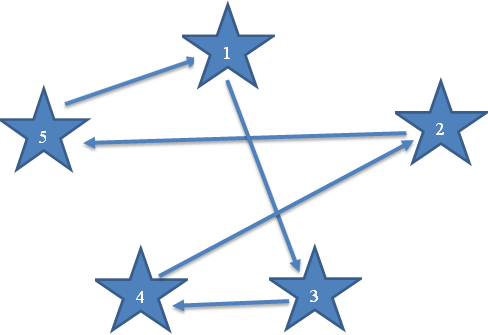
Рисунок 2.1.10 – Схема кольцевого маршрута методом ветвей

Выбираем четвёртое наибольшее значение и осуществляем ветвление. Наибольшее значение Q1.4. Столбец и строка данного элемента вычеркивается, в клетке Q4.1 ставится бесконечность и составляется ветвление.

 Таблица 2.1.13 - Приведенная матрица (вторая итерация)

Пункты начала движения	Пункты конца движения
1	2	3	4
1	∞	0	0	0
3	0	1	∞	4
4	16	0	1	∞
5	0	∞	5	1

Q3.1=0+1=1 (1)                                    Q1.3=0+1=1 (3)

Q5.1=0+1=1 (2)                                    Q1.4=1+0=1 (4)

Q1.2=0+0=0                                          Q4.2=0+1=1 (5)

 

                   43                                           41

 

                                               42                                     41

Рисунок 2.1.11 Начало ветвления дуги 1.4

Рассчитываем нижние границы подмножества.

h 2=0            h1+h2=41+0=41            h1+h2+Q1.4=41+0+1=42

Таблица 2.1.14 - Приведенная матрица (третья итерация)

Пункты начала движения	Пункты конца движения
1	2	3
3	0	1	∞
4	∞	0	1  0
5	0	∞	5  4

·                          Сумма констант приведения = 0. Сделав нули в необходимой строке, рассчитываем для всех нулевых элементов приведенной матрицы значения Q(i и j). Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q(i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца, исключая «0» находящихся в i-строке и в j-столбце.

Q3.1=0+1=1                                   Q4.2=0+1=1                                    

Q5.1=0+4=4                                       Q4.3=0+1=1

Рассчитываем нижние границы подмножества.

h 3=1     h1+h2+h3=41+0+1=42            h1+h2+Q5.1=41+0+4=45

·                          Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q(i и j). Определяется как сумма минимального элемента i-строки и минимального элемента j-столбца, исключая «0» находящихся в i-строке и в j-столбце.

 

         43                                                41

 

                                          42                                       41

 

45                        42

 

Рисунок 2.1.12 Начало ветвления дуги 5.1

Таблица 2.1.15 - Приведенная матрица (четвёртая итерация)

Пункты начала движения	Пункты конца движения
2	3
3	0	∞
4	0	0

На этом ветвление заканчивается. Включение в варианты дуг Q_4.3 и Q_3.2 образуют дерево.

Полученный вариант: Z (2.5, 1.4, 5.1, 4.3, 3.2)

Затраты времени в четвёртом варианте составили 45 минут.

 

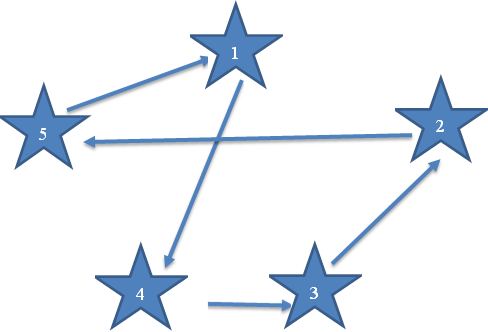
Рисунок 2.1.13 – Схема кольцевого маршрута методом ветвей

Выбираем пятое наибольшее значение и осуществляем ветвление. Наибольшее значение Q4.2. Столбец и строка данного элемента вычеркивается, в клетке Q2.4 ставится бесконечность и составляется ветвление.

Таблица 2.1.16 - Приведенная матрица (вторая итерация)

Пункты начала движения	Пункты конца движения
1	2	3	4
1	∞	0	0	0
3	0	1	∞	4
4	16	0	1	∞
5	0	∞	5	1

·                          Сумма констант приведения = 0. Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q(i и j).

Q3.1=0+1=1 (1)                                    Q1.3=0+1=1 (3)

Q5.1=0+1=1 (2)                                    Q1.4=1+0=1 (4)

Q1.2=0+0=0                                          Q4.2=0+1=1 (5)

 

                   43                                           41

 

                                               42                                  41

Рисунок 2.1.14 Начало ветвления дуги 4.2

Рассчитываем нижние границы подмножества.

h 2=0            h1+h2=4+0=41              h1+h2+Q4.2=41+0+1=42

Таблица 2.1.17 - Приведенная матрица (третья итерация)

Пункты начала движения	Пункты конца движения
1	3	4
1	∞	0	0
3	0	∞	4
5	0	5	1

·                          Сумма констант приведения = 0. Для каждой клетки содержащей «0» приведенной матрицы в правом верхнем углу клетки записываем значения Q(i и j).

Q3.1=0+4=4                                   Q1.3=0+4=4                                    

Q5.1=0+5=5                                       Q1.3=0+4=4

Рассчитываем нижние границы подмножества.

h 3=0            h1+h2+h3=41+0+0=41                      h1+h2+Q5.1=41+0+5=46

 

                       43                                                    41

                                                        42                        41    

 

46                                 41

Рисунок 2.1.15 Начало ветвления дуги 5.1

Таблица 2.1.18 - Приведенная матрица (четвёртая итерация)

Пункты начала движения	Пункты конца движения
3	4
1	0	0
3	∞	0

На этом ветвление заканчивается. Включение в варианты дуг Q_1.3 и Q_3.4 образуют дерево.

Полученный вариант: Z (2.5, 4.2, 5.1, 1.3, 3.4)

Затраты времени в пятом варианте составили 41 минута.

 

Рисунок 2.1.16 – Схема кольцевого маршрута методом ветвей

Вывод: Данный вариант получился наиболее оптимальным из пяти предложенных вариантов. Затраты времени при расчете методом ветвей и границ получились минимальными, и составили 41 минуту. Рассмотренный метод «Ветвей и границ» является точным и обеспечивает возможность получения оптимального маршрута, однако, применение этого метода без электронных средств требует проведения громоздких расчетов.

2.2 Метод Дакея

Метод Дакея может быть использован для приближенных расчетов кольцевых маршрутов.

Рассмотрим пример на данном этапе.

Метод предусматривает последовательное вычеркивание наибольших значений элементов матрицы:

Таблица 2.2.1 - Исходные данные

Пункты начала движения	Пункты конца движения
1	2	3	4	5
1	∞	5	4	5	23
2	8	∞	8	8	5
3	6	8	∞	11	12
4	26	11	11	∞	10
5	14	16	19	16	∞

1. Максимальные значения в матрице: 26, 23, 19, 16, 16 они вычеркиваются. В 5 строке остается один не вычеркнутый элемент - Q5.1, он округляется, столбец 1 вычеркивается и элемент Q1,5 также вычеркивается.

2. Затем максимальные значения в матрице:12, 11, 11, 11 они вычеркиваются и в 4 строке остается один не вычеркнутый элемент - Q4.5, он округляется, столбец 5 вычеркивается и элемент Q5.4 также вычеркивается.

3. После этого в 3 строке остается один не вычеркнутый элемент - Q3.2, он округляется, столбец 2 вычеркивается и элемент Q2.3 также вычеркивается.

4. В 2 строке остается один не вычеркнутый элемент- Q2.4, он округляется, столбец 4 вычеркивается и элемент Q4.2 также вычеркивается.

5. В 1 строке в окончательном итоге остаётся один не вычеркнутый элемент, и он округляется.

Протяженность маршрута будет равна:

Z(5.1; 3.2; 4.5; 2,4; 1.3) = 14+8+10+8+4=44 минут.

 

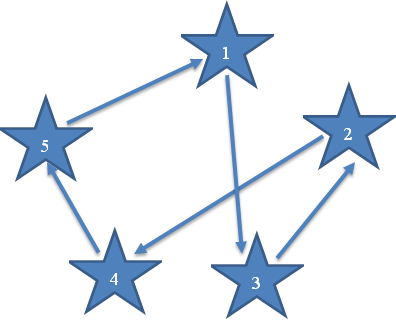
Рисунок 2.2.1 – Схема маршрута методом Дакея

Вывод: При расчете данным методом затраты времени составили 44 минуты, а это значит, что метод Дакея в данном варианте не является самым оптимальным способом решения.

2.3 Метод Дакея-Габра

Данный метод является более строгим по сравнению с методом Дакея и обеспечивает решение более близким к оптимальному. По этому методу таблица значений преобразуется. В основу берутся отклонения от средних значений по столбцу и строке. В остальном схема расчета остается не изменой. (используется метод Дакея).

Расчет элементов матрицы ведется по формуле:

               f(ij) = 2d(ij)-Z(i)-S(j),                                                        (2.3.1)

где f (ij) – величина элемента i-строки и j- столбца по методу Дакея-Габра

d (ij) – длина частичного маршрута

Z (i) – среднее значение расстояния (времени) по i-строке

S (j) – среднее значение (времени) по j-столбцу

Среднее значение определяется по формуле:

    Z(i),S(j) = (2.3.2)

Таблица 2.3.1 - Исходные данные

Пункты начала движения	Пункты конца движения	Zi
1	2	3	4	5
1	∞	5	4	5	23	9,25
2	8	∞	8	8	5	7,25
3	6	8	∞	11	12	9,25
4	26	11	11	∞	10	14,50
5	14	16	19	16	∞	16,25
Sj	13,5	10,0	10,5	10,0	12,5

f_1.2 = 2 * 5 – 9, 25 – 10, 0 = -9, 25                      f_1.3 = 2 * 4 - 9, 25 - 10, 5 = -11, 75

f_1.4 = 2 * 5 – 9, 25[A2]  – 10, 0 = -9, 25                           f_1.5 = 2 * 23 - 9, 25 - 12, 5 = 24, 25

f_2.1 = 2 * 8 - 7, 25 - 13, 5= -4, 75                         f_2.3 = 2 * 8 - 7, 25 - 10, 5 = -1, 75

f_2.4 = 2 * 8 - 7, 25 – 10, 0 = -1, 25                       f_2.5 = 2 * 5 - 7, 25 - 12, 5 = -9, 75

f_3.1 = 2 * 6 - 9, 25 - 13, 5 = -10, 75                      f_3.2 = 2 * 8 - 9, 25 – 10, 0 = -3, 25

f_3.4 = 2 * 11 - 9, 25 – 10, 0 = 2, 75                      f_3.5 = 2 * 12 - 9, 25 - 12, 5 = 2, 25

f_4.1 = 2 * 26 - 14, 50 - 13, 5 = 24                         f_4.3 = 2 * 11 - 14, 50 - 10, 5 = -3

f_4.2 = 2 * 11 - 14, 50 – 10, 0 = -2, 5                     f_4.5 = 2 * 10 - 14, 50 - 12, 5 = -7, 0

f_5.1 = 2 * 14 - 16, 25 - 13, 5 = -1, 75                    f_5.3 = 2 * 19 - 16, 25 - 10, 5 = 11, 25

f_5.2 = 2 * 16 - 16, 25 - 10, 0 = 5, 75                     f_5.4 = 2 * 16 - 16, 25 – 10, 0 = 5, 75

Таблица 2.3.2 – Следующий этап решений

Пункты начала движения	Пункты конца движения
1	2	3	4	5
1	∞	-9,25	-11,75	-9,25	24,25
2	-4,75	∞	-1,75	-1,25	-9,75
3	-10,75	-3,25	∞	2,75	2,25
4	24,00	-2,50	-3,20	∞	-7,00
5	-1,75	5,75	11,25	5,75	∞

1. Максимальные значения в матрице: 24.25, 24,00, 11.25, 5.75, 5.75, они вычеркиваются.

2. В 5 строке остается один не вычеркнутый элемент - Q5.1, он округляется, столбец 1 вычеркивается и элемент Q1,5 также вычеркивается.

3. Максимальные значения в матрице: 2.75, 2.25, -1.25 они вычеркиваются.

4. В 1 строке остается один не вычеркнутый элемент - Q1.4, он округляется, столбец 4 вычеркивается и элемент Q4.1 также вычеркивается.

5. В 3 строке остается один не вычеркнутый элемент- Q3.2, он округляется, столбец 2 вычеркивается и элемент Q2.3 также вычеркивается.

6. В 4 строке остается один не вычеркнутый элемент- Q4.3, он округляется, столбец 3 вычеркивается и элемент Q3.4 также вычеркивается.

7. В 2 строке в окончательном итоге остаётся один не вычеркнутый элемент, и он округляется.

Протяженность маршрута будет равна:

Z(5,1; 3,2; 4,3; 1,4; 2,5) = 14+8+11+5+5=43 минуты.

 

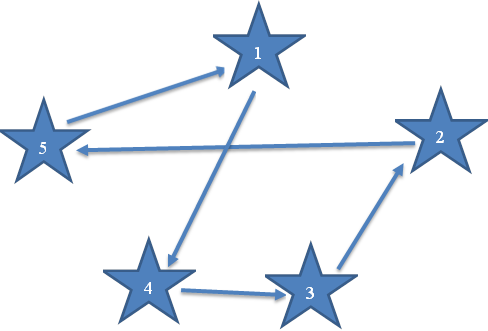
Рисунок 2.3.1 – Схема маршрута методом Дакея-Габра

Вывод: При расчете данным методом затраты времени составили 43 минуты, а это значит, что метод Дакея-Габра в данном варианте не является самым оптимальным способом решения.

.

ЗАКЛЮЧЕНИЕ

В данной курсовой работе использовались три метода для расчета затрат времени: метод ветвей границ, метод Дакея и метод Дакея-Габра.

При расчете методов ветвей границ было 5 вариантов использования разных дуг для расчета затрат времени. Варианты, где использовалась дуги 3.1. 5.1. и 1.4. не целесообразно использовать, т.к. время при использовании данных дуг по правой ветке начало увеличиваться (стало 42 минуты), когда до этого время было 41 минута. При использовании дуги 1.3. стало понятно, что этот вариант не стоит рассматривать, так как там время ещё больше увеличивается (43 минуты). А вот при использовании дуги 4,2 время составило 41 минуту и на протяжении решения не увеличивалось. Следовательно, последний (пятый) вариант с использованием дуги 4,2 целесообразно использовать.

При расчете методом Дакея затраты времени составили 44 минуты. В данном методе был один вариант использования дуги для расчета.

При расчете третьим методом Дакея-Габра затраты времени составили немного меньше, чем при расчёте методом Дакея 43 минуты.

Исходя из этого можно сделать общий вывод.

Вывод: Кольцевой маршрут в данном случае лучше прокладывать воспользовавшись методом ветвей и границ, с использованием дуги 4.2., так как время на затраты составило 41 минуту. Всё это даёт возможность сократить 1 работника, что позволит уменьшить расходы на топливо и заработную плату.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1  Шалимо Т. Ю. Организация почтовой связи: учебн. пособие / Т. Ю. Шалимо, Ю. Д. Пашковская. Минск: УО ВГКС, 2012. 198 с.

2  Инструкция о порядке расчета и размещения объектов почтовой связи и почтовых ящиков на территории Республики Беларусь: Приказ Министерства связи и информатизации Республики Беларусь от 28.10.2009 № 310, Минск: МС и ИРБ, 2009.

3  Министерство связи и информатизации Республики Беларусь [Электронный ресурс]. – Режим доступа: http://www.mpt.gov.by/ru. – Дата доступа: 03. 03. 2014.

4  О почтовой связи: Закон Респ. Беларусь: [Принят Палатой представителей 12 нояб. 2003 г.: Одобр. Советом Респ. 28 нояб. 2003 г., № 258-З - Мн.: БДП, [2003]. - 24 с.

5 Почтовая связь // Министерство связи и информатизации Республики Беларусь [Электронный ресурс]. – Режим доступа: http://www.mpt.gov.by/ru/new_page_4_3_15089. – Дата доступа: 03. 03. 2014.

6  Правила оказания услуг почтовой связи: постановление Совета Министров Респ. Беларусь, 07 сент. 2004 г. № 1111 // Нац. реестр правовых актов Респ. Беларусь. – 2004. - № 2. - 2/1007.

ПРИЛОЖЕНИЕ А

Схема оптимального кольцевого маршрута методом ветвей и границ