Линейные электрические цепи постоянного тока.

Приднестровский государственный университет им. Т. Г. Шевченко

Физико-математический факультет

Кафедра твердотельной электроники и микроэлектроники

Курсовая работа

По дисциплине: «Теоретические основы электротехники»

Тема: «Линейные электрические цепи постоянного тока. Расчёт линейной электрической цепи синусоидального тока с сосредоточенными параметрами при установившемся режиме»

Выполнил

студент 212 группы

Муратова Ю. А.

Проверил

ст. преподаватель

кафедры ТТЭМ

Чукита В. И.

Тирасполь 2016

Оглавление

ЗАДАНИЕ 1. 3

1.Упрощение сложной электрической цепи. 4

2. Расчет преобразованной электрической цепи. 5

2.1 Метод наложения действий э. д. с. 5

2.2 Метод эквивалентного генератора. 7

3. Определение токов и их направлений. Построение потенциальной диаграммы. 9

4. Определение коэффициентов четырёхполюсника. 10

ЗАДАНИЕ 2. 15

Часть 1. 16

1. Определение показаний приборов. 16

2. Построение векторных диаграмм.. 17

4. Баланс активной и реактивной мощности. 19

5. Резонанс напряжений. 19

6. Резонанс токов. 20

Часть 2. 21

1. Определение комплексов токов в ветвях и комплексы напряжений для всех ветвей цепи  21

2. Векторная диаграмма напряжений и токов. 21

3. Мгновенные значения напряжений и токов. 22

4. Комплексы мощностей всех ветвей. 23

5. Показания ваттметров в 3-ей и 4-ой ветвях. 23

Вывод. 23

Список литературы.. 24

ЗАДАНИЕ 1

Расчет линейной электрической цепи

Вариант 6

Исходные данные:

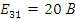
Рис. 1. Линейная электрическая цепь постоянного тока

1.      Упростить сложную электрическую цепь (рис. 1), используя метод преобразования треугольника и звезды. Определить токи во всех ветвях сложной цепи (рис.1), используя следующие методы:

Метод преобразования треугольника и звезды.

2.      Преобразованную электрическую цепь рассчитать:

Методом наложения действий э. д. с.

Методом эквивалентного генератора (определить ток в ветви без э. д. с.).

3.      Определить токи, направление токов и построить потенциальную диаграмму для одного из контуров схемы с двумя э. д. с.

4.      Определить коэффициенты четырёхполюсника, считая входными и выходными зажимами зажимы, к которым подключены ветви с э. д. с, и параметры Т-образной и П-образной эквивалентных схем замещения этого четырёхполюсника.

1.Упрощение сложной электрической цепи

Для упрощения сложной электрической цепи (рис. 1), необходимо выбрать контур, содержащий пассивные элементы. В данном случае подходит способ преобразования треугольника в звезду (рис. 2).

Рис. 2.

После преобразования цепь примет вид (рис. 3).

Рис. 3. Преобразованная цепь.

Где 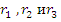находятся по формулам

2. Расчет преобразованной электрической цепи 2.1 Метод наложения действий э. д. с.

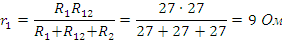
Принцип действия метода наложений действий э. д. с. заключается в том, что в любой ветви схемы ток можно определить, как результат наложения частных токов, получающихся в этой ветви от каждой ЭДС в отдельности. Для определения частных токов на основании исходной схемы (рис. 3) нужно составить частные схемы, в каждой из которых действует одно ЭДС. Получим следующие схемы (рис. 4а, б)

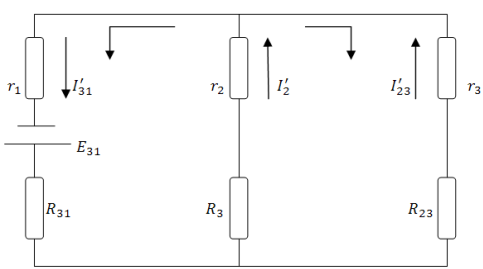
а)

б)

Рис.4. Частные схемы

Из рис. 4 (а, б) видно, что

Найдем токи в частных схемах методом контурных токов

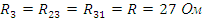
а)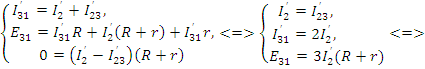

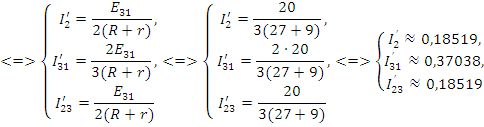
б)

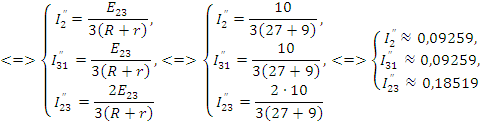
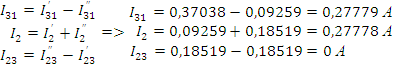
Для того чтобы убедиться в правильности решения произведем проверку по балансу мощностей.

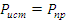
Так как мощность источника тока равна мощности приёмника следует, что найденное решение верно.

2.2 Метод эквивалентного генератора

Суть метода эквивалентного генератора заключается в том, что он даёт возможность определить ток в отдельно взятой пассивной цепи (не имеющей источника ЭДС), не вычисляя токи в других ветвях.

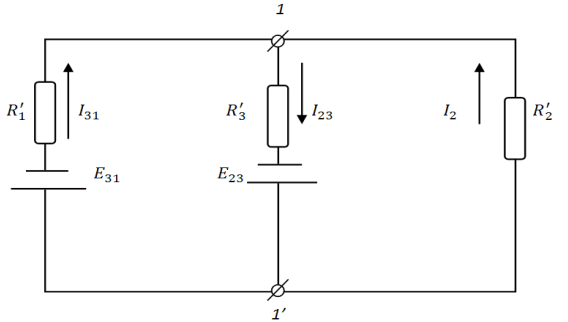
Рис. 5. Расчёт цепи методом эквивалентного генератора

Ток   может быть рассчитан по закону Ома

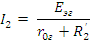
где  .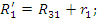

Для определения этого тока необходимо знать ЭДС эквивалентного генератора и его внутреннее сопротивление учитывая, что  известно. Параметры  и 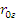 могут быть найдены путем рассмотрения режимов холостого хода (ХХ) и короткого замыкания (КЗ).

Рис. 6. Схема в режиме ХХ

Находим  в режиме ХХ

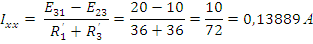
Рис. 7. Схема в режиме КЗ

Найдем в режиме КЗ, применив первый закон Кирхгофа

где

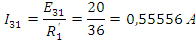
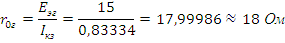
Зная 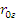 и  определим ток в ветви

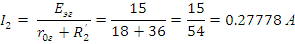
Данное значение тока, полученное методом эквивалентного генератора, соответствует значению того же тока, полученное методом наложения действий ЭДС, следовательно, решение верно

3. Определение токов и их направлений. Построение потенциальной диаграммы.

В целях упрощения исследования электрических цепей и анализа режима их работы, строят потенциальные диаграмы данных цепей. Потенциальной диаграмой называют графическое изображение распределения потенциалов в электрической цепи в зависимости от сопротивления её элементов.

Рис. 8. Схема электрической цепи

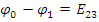
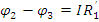
Так как точка 0 заземлена , отсюда следует, что

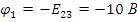
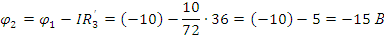
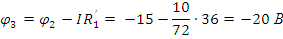
Проверка расчетов проводится следующим образом

 расчеты верны.

По данным значениям потенциалов построим диаграмму

Рис. 9. Потенциальная диаграмма.

4. Определение коэффициентов четырёхполюсника

Метод четырёхполюсника применяется при необходимости исследования изменения режима одной ветви при изменении электрических характеристик в другой ветви.

Четырёхполюсником называется часть схемы электрической цепи между двумя парами точек, к которым присоединены две ветви. Чаще всего встречаются схемы, в которых одна из ветвей содержит источник, а другая приёмник. Зажимы, к которым присоединяется участок цепи с источником, называются входными, а зажимы, к которым присоединяется приёмник - выходными. Четырёхполюсник, который состоит только из пассивных элементов – пассивный. Если в схему четырёхполюсника входит хоть одна ветвь с ЭДС, то он называется активным.

Напряжения и токи ветвей, включенных к входным и выходным зажимам четырёхполюсника, связаны между собой линейными соотношениями, если вся электрическая цепь состоит и линейных элементов. Так как переменными являются  то уравнения, связывающие их, должны предусматривать возможность нахождения двух из них, когда два других известны. Число сочетаний из четырёх по два равно шести, т.е. существуют шесть форм записи уравнений. Основной формой записи является А-форма:

где - напряжения и токи на входе и выходе четырёхполюсника;

- постоянные четырёхполюсника, зависящие от конфигурации схемы и величин, входящих в неё сопротивлений.

Задача исследования режима ветви на выходе четырёхполюсника в связи с режимом на входе сводится на первом этапе к определению его постоянных. Их измеряют расчётным путем или измерением.

Рис. 10. Схема с пассивным Т-образным четырёхполюсником.

Для расчета рассмотрим режимы ХХ и КЗ на выходных зажимах.

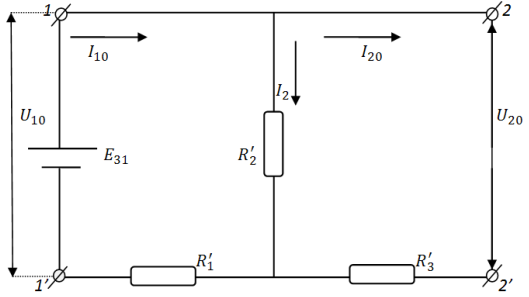
Рис. 11.Схема Т-образного четырёхполюсника в режиме ХХ.

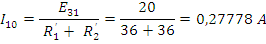
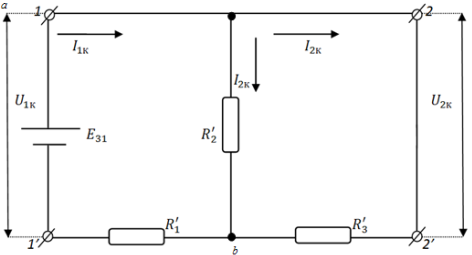
Рис. 12.Схема Т-образного четырёхполюсника в режиме КЗ.

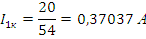
Определим коэффициенты четырёхполюсника

При ХХ:

При КЗ:

Так как , следует, что четырёхполюсник является симметричным, т.е. при перемене источника и приёмника местами, токи на входе и выходе четырёхполюсника не изменяются. Для любого четырёхполюсника справедливо соотношение:

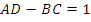
Подставив найденные коэффициенты в это соотношение получим:

Известно, что Т-образную схему замещения (звезда) сопротивлений 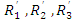 можно заменить эквивалентным треугольником . После такой замены получим П-образную схему замещения пассивного четырехполюсника.

Рис. 13. П-образная схема замещения пассивного четырехполюсника

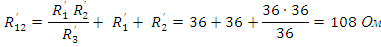
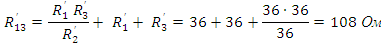
Коэффициенты для П-образной схемы замещения пассивного четырёхполюсника вычисляются по следующим формулам:

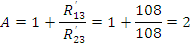
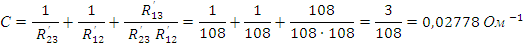
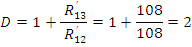
Параметры схем замещения и постоянные четырёхполюсника связаны соответствующими формулами. Из них нетрудно найти сопротивления Т-образной и П-образной схем замещения и таким путем перейти от любой заданной схемы пассивного четырёхполюсника к одной из эквивалентных схем.

Параметры Т-образной схемы можно найти через соответствующие коэффициенты:

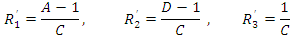
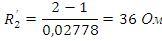
Параметры П-образной схемы:

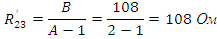
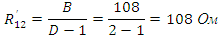
ЗАДАНИЕ 2

Расчет линейной электрической цепи синусоидального тока с сосредоточенными параметрами при установившемся режиме

Вариант 6

Исходные данные:

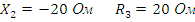
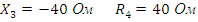
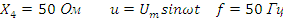
Рис. 14. Линейная электрическая цепь синусоидального тока.

Часть 1

1.      Определить показания всех приборов, указанных на схеме.

2.      Построить векторные диаграммы токов и напряжений.

3.      Написать мгновенные значения токов и напряжений.

4.      Составить баланс активной и реактивной мощности.

5.      Определить для данной цепи индуктивность , при которой будет иметь место резонанс напряжений.

6.      Определить емкость 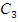, при которой в ветвях 3-4 наблюдается резонанс токов.

Часть 2

1.      Определить комплексы токов в ветвях и комплексы напряжений для всех ветвей цепи (рис. 14).

2.      Построить в комплексной плоскости векторную диаграмму напряжений и токов.

3.      Написать выражения мгновенных значений, найденных выше напряжений и токов.

4.      Определить комплексы мощностей всех ветвей.

5.      Определить показания ваттметров, измеряющих мощности в 3-ей и 4-ой ветвях.

Часть 1 1. Определение показаний приборов

Преобразуем цепь и определим показания всех приборов:

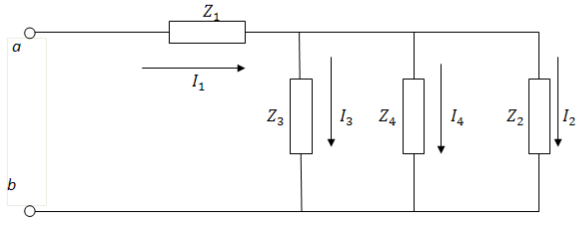
Рис. 15. Преобразованная электрическая цепь синусоидального тока

Из рисунка видно, что

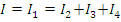
Найдем полные сопротивления соответствующих ветвей:

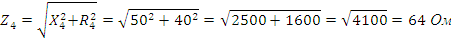
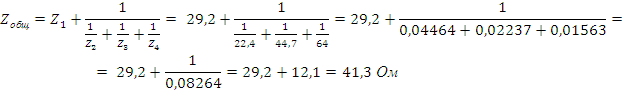
Найдем токи и напряжения:

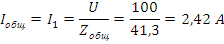
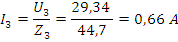
Из выше приведенных вычислений, определим показания приборов:

2. Построение векторных диаграмм

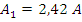
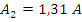
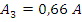
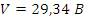
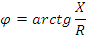
Рис. 16. Векторная диаграмма токов.

 

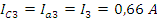
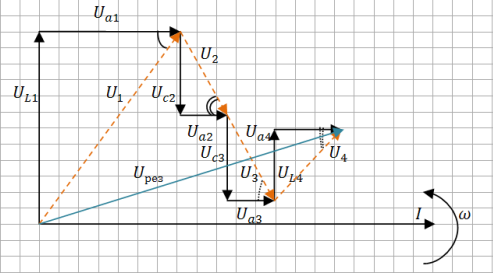
Рис. 17. Векторная диаграмма напряжений.

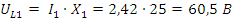
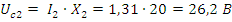
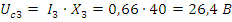
Из диаграмм видно, что цепь носит преимущественно индуктивный характер.

  3. Мгновенные значения токов и напряжений

4. Баланс активной и реактивной мощности

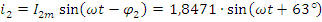
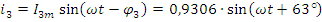
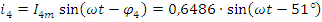
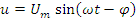
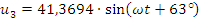
Для проверки расчёта тока в ветвях, составим баланс мощностей для схемы

5. Резонанс напряжений

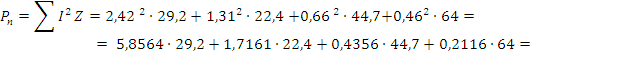
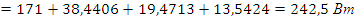
Резонанс напряжений возникает в цепи с последовательным соединением индуктивного и емкостного элемента, когда частота источника совпадает с частотой резонанса и равенстве реактивных сопротивлений индуктивного и емкостного элемента, т.е.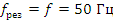

Рис. 18. Преобразованная цепь при резонансе напряжений.

Найдем емкость преобразованной цепи:

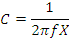
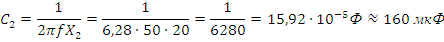
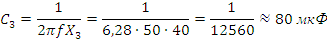
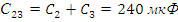
Зная частоту и емкость цепи, найдем индуктивность , при которой будет иметь место резонанс напряжений.

6. Резонанс токов

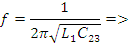
Резонанс токов возникает в цепи с параллельным соединением индуктивного и емкостного элемента, когда частота источника совпадает с частотой резонанса и равенстве реактивных сопротивлений индуктивного и емкостного элемента, т.е.

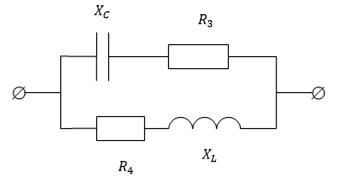
Рис. 19. Ветви 3-4 при резонансе токов.

Найдем индуктивность в ветвях 3-4:

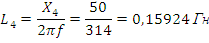
Зная частоту и индуктивность, найдем емкость , при которой в ветвях 3-4 наблюдается резонанс токов.

Часть 2 1. Определение комплексов токов в ветвях и комплексы напряжений для всех ветвей цепи

2. Векторная диаграмма напряжений и токов

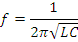
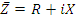
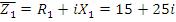
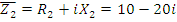
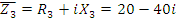
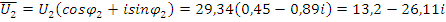
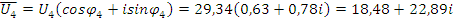
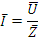
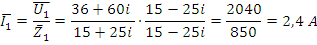
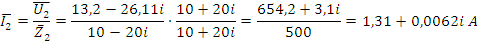
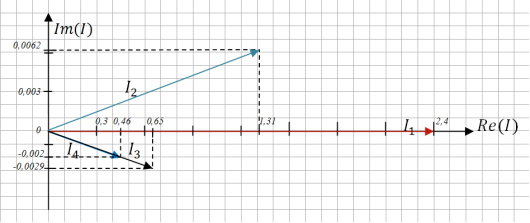
Рис. 20. Векторная диаграмма токов в комплексной плоскости.

Рис. 21. Векторная диаграмма напряжений в комплексной плоскости.

3. Мгновенные значения напряжений и токов

4. Комплексы мощностей всех ветвей

5. Показания ваттметров в 3-ей и 4-ой ветвях

Вывод

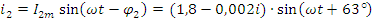
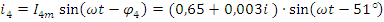
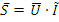
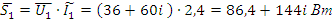
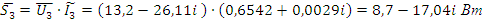
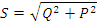
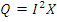
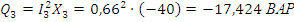
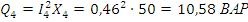
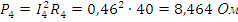
В данной курсовой работе были рассмотрены методы расчёта линейных электрических цепей постоянного тока, определения параметров методами: наложения действий ЭДС и эквивалентного генератора. Определены параметры четырехполюсника схемы, построена потенциальная диаграмма для одного из контуров схемы с двумя ЭДС. Был произведен расчет электрической цепи синусоидального тока, определены показания всех приборов, построены векторные диаграммы токов и напряжений. Составлен баланс активной и реактивной мощности, так же были определены комплексы токов и напряжений для всех ветвей цепи, построена в комплексной плоскости векторная диаграмма токов и напряжений и найдены мгновенные значения напряжений и токов.

Список литературы

1.      В.М. Ишимов, В.И. Чукита, методические указания к курсовой работе по расчёту линейных электрических цепей постоянного тока. Научно-методическим советом ПГУ им. Т.Г. Шевченко г. Тирасполь 2013

2.      Евдокимов А.М. Теоретические основы электротехники. 1982г.

3.      Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1996, 637 с.

4.      Попов В.П. Основы теории цепей. – М.: Высшая школа, 1985, 488с.