Использование алгебры высказываний

ОГБОУ СПО «Политехнический техникум г. Рязани»

РЕФЕРАТ

по дисциплине:

 «Элементы математической логики»

на тему:

«Использование алгебры высказываний в

 вычислительной технике»

Выполнил:

Батьков В.А.

Проверила:

Лукьянова А.П.

2012

 

Содержание

Использование алгебры логики в вычислительной технике.............................................3

Алгебра переключательных схем............................................................................
.........3

Логические элементы........................................................................
.............................9

Комбинационные схемы...........................................................................
......................9

Синтез комбинационных схем............................................................................
...........10

Примеры комбинационных схем............................................................................
.......11

Список рекомендуемой литературы......................................................................
.........15

1. Использование алгебры логики

в вычислительной технике

            При разработке вычислительной техники широкое применение находит алгебра логики. Любая информация может быть представлена дискретным сигналом — в виде фиксированного набора отдельных значений. Устройства, в которых действуют такие сигналы, называются дискретными.
            Всякий преобразователь информации — некая искусственная система обработки информации, устройство, имеющее входы и выходы. Простейшими преобразователями информации являются логические преобразователи дискретного действия. Их условное обозначение:




Здесь А₁, А₂, ..., А_n — входы, X₁, Х₂, ... , Х_n — выходы.
На каждый вход подаются сигналы только двух видов, обозначаемые 0 и 1. Такие же сигналы появляются на каждом выходе.
                  2. Алгебра переключательных схем

            Долгое время алгебра логики была известна достаточно «узкому» классу специалистов. Прошло почти 100 лет, прежде чем в 1938 году выдающийся американский математик и инженер Клод Шеннон обнаружил, что алгебра логики применима для описания самых разнообразных процессов. Например, 0 и 1 могут кодировать включенные и выключенные переключатели, высокое и низкое напряжение, годную и бракованную продукцию и т. д.
            Прежде всего алгебра логики была использована для преобразования релейно-контактных и электронно-ламповых схем. Отвлекаясь от физической природы этих схем, будем называть их переключательными. Другими словами, под переключательной схемой мы будем понимать схематическое изображение какого-либо устройства, содержащего только двухпозиционные переключатели, т. е. переключатели, которые могут находиться только в двух состояниях: в замкнутом (ток проходит) и в разомкнутом (ток не проходит).
            2.1. Связь между переключательными схемами

и алгеброй высказываний

            Любую переключательную схему можно разбить на участки из последовательно или параллельно соединенных переключателей. Каждому переключателю поставим в соответствие элементарное высказывание, истинное тогда, когда переключатель замкнут, и ложное, если переключатель разомкнут. На схемах переключатели будем обозначать теми же буквами, что и соответствующие им элементарные высказывания. Если в цепи содержится несколько переключателей А, то все эти переключатели должны быть одновременно замкнуты или разомкнуты.
           

Переключателям, соединенным параллельно, поставим в соответствие операцию дизъюнкции: ток в этой цепи (рис. 1, а) будет протекать при замкнутом переключателе А, или переключателе В, или замкнутых переключателях А и В одновременно.

а	б
Рис. 1

            Переключателям, соединенным последовательно, поставим в соответствие операцию конъюнкции: ток в цепи (рис. 1, б) потечет только тогда, когда замкнут переключатель А и замкнут переключатель В.
            Если два переключателя работают так, что один из них замкнут, когда другой разомкнут и наоборот, то им ставятся в соответствие высказывания А и А.
            2.2. Чтение и анализ переключательных схем

    Прочитать переключательную схему — это значит определить, протекает по ней ток или нет при определенных состояниях переключателей.
Пример. Дана схема:

Состояния переключателей задаются таблицей:

А	B	C	Состояние схемы
0	0	1
1	1	0
1	1	1

Требуется прочитать переключательную схему — заполнить колонку «Состояние схемы». Будем последовательно рассматривать все строки таблицы, описывающие состояние переключателей данной схемы.
   1. Переключатели А и В разомкнуты, С замкнут. В этом случае ток не может проходить ни по одной из двух цепочек параллельного соединения. Состояние схемы 0.
   2. Так как переключатель А замкнут, ток будет проходить по верхней цепочке параллельного соединения. Состояние схемы 1.
   3. Ток может проходить по обеим цепочкам параллельного соединения. Состояние схемы 1.
            Две схемы, содержащие одни и те же переключатели А, В,..., мы будем считатьодинаковыми или равными, если при одном и том же состоянии переключателей (А замкнут, В разомкнут и т. д.) обе схемы одновременно пропускают или не пропускают ток. Естественно считать из двух схем более простой ту, которая содержит меньше переключателей.

В алгебре «переключательных схем» выполняются все законы алгебры логики. В этом достаточно просто убедиться, если прочитать приведенные ниже схемы и сравнить столбец состояния каждой схемы с результирующим столбцом таблицы истинности для соответствующей логической формулы.
            Справедливость коммутативного закона для параллельного и последовательного соединения контактов видна на рис. 1, ассоциативного закона — на рис. 2.

Рис. 2

Равенство схем, приведенных на рис. 3 и 4, говорит о справедливости дистрибутивного закона.

Рис. 3

Рис. 4

На рис. 5 приведены переключательные схемы, реализующие следующие соотношения:

a) Ú в) Ú д) ж)

б) Ú г) Ú е) з)

Рис. 5

            2.3. Упрощение переключательных схем

      Каждой переключательной схеме можно поставить в соответствие сложное высказывание, истинное тогда и только тогда, когда схема проводит ток. Это сложное высказывание можно исследовать методами математической логики. Если такое сложное
высказывание удается упростить, то и соответствующая схема допускает аналогичное упрощение.

Пример 1. Составим формулу логической функции для следующей схемы. Переключатели А и В соединены параллельно, что соответствует дизъюнкции соответствующих высказываний: A v В. Далее следует последовательное соединение с переключателемС:

(А v В) & С. Рассмотренный участок цепи параллельно соединяется с переключателем D: (А v В) & С v D.
           

Окончательный результат: F(A,B,C,D) = (А v В) & C v D.
           

Анализ переключательной схемы состоит в определении всех возможных условий, при которых соответствующая электрическая цепь будет пропускать электрический ток. Это удобно делать с помощью соответствующей логической функции.
            2.4. Алгоритм анализа переключательной схемы

   1. Записать логическую формулу, соответствующую данной переключательной схеме.
  2. По полученной формуле построить таблицу истинности.
 3. Выбрать в таблице истинности наборы (строки), где функция принимает единичные значения. Единицы в рассматриваемых наборах соответствуют замкнутым переключателям, а нули — разомкнутым.
            Пример 2. Проанализируем переключательную схему из предыдущего примера.

1. ÚÚ

2.

3. Электрическая цепь пропускает ток, если состояния переключателей соответствуют наборам: 0001, 0011, 0101, 0110, 0111, 1001, 1010, 1011, 1101, 1110, 1111.

Синтез переключательной схемы — это разработка схемы, условия работы которой заданы таблицей истинности или словесным описанием.

Пример. Построим схему электрической цепи, включающей переключатели А, В, С, такую, что цепь замыкается лишь в том случае, если замкнуты все переключатели или ни один из этих переключателей.

Решение. Оформим в виде таблицы все возможные соположения переключателей А, В, С и в отдельном столбце отметим требуемое состояние для каждого набора состояний переключателей:

Построим СДНФ: F(A,B,C)=A & B & C V A & B & С. Этой логической функции соответствует переключательная схема:



Упрощение (минимизация) переключательной схемы сводится к упрощению соответствующей ей формулы на основании законов алгебры логики.
Пример. Упростить схему:

Решение. Исходная схема имеет девять переключателей.
Выпишем логическую формулу, соответствующую данной схеме и упростим ее.
ÚÚÚ =
ÚÚÚÚÚ
Ú
ÚÚÚÚ
ÚÚÚÚ
Рассматриваемая схема может быть заменена более простой, содержащей только три включателя

            3. Логические элементы

Дискретный преобразователь, который выдает после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом.
Ниже приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и отрицание.



Логический элемент И (конъюнктор) реализует операцию -логического умножения. Единица на выходе этого элемента будет только тогда, когда на всех входах будут единицы. Если хотя бы на одном входе будет нуль, на выходе также будет нуль.

Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения. Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица.

Знак 1 на схеме элемента — остаток устаревшего обозначения операции ИЛИ (результат операции ИЛИ равен единице, если сумма значений операндов больше или равна 1).

Логический элемент НЕ (инвертор) реализует операцию отрицания. Если на входе элемента нуль, то на выходе единица; если на входе элемента единица, то на выходе нуль.

Описанные логические элементы могут быть реализованы многими способами — на пневматической, гидравлической, механической или электрической основе. Важно лишь, чтобы нули и единицы на входе были идентичны нулям и единицам на выходе.

Любой преобразователь информации, имеющий п входов и т выходов, можно заменить набором из т преобразователей,
каждый из которых имеет п входов и один выход.

Следовательно, для построения произвольного преобразователя информации достаточно уметь синтезировать преобразователи с одним выходом.
            4. Комбинационные схемы

Схему преобразователя информации, сигнал на выходе которой однозначно определяется комбинацией сигналов на входах, называют комбинационной.

Однотипность сигналов на входах и выходах позволяет подавать сигнал, вырабатываемый одним элементом, на вход другого элемента. Это позволяет из двухвходовых схем И и ИЛИ строить многовходовые схемы, а также синтезировать произвольные комбинационные схемы, соединяя в цепочки отдельные логические элементы.

Пример 1. Покажем, как из двухвходовых схем И можно построить схему И с любым количеством входов.


Анализируя комбинационную схему, можно понять, как работает логическое устройство.
Пример 2. Проанализируем комбинационную схему, т. е. выясним, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входе.

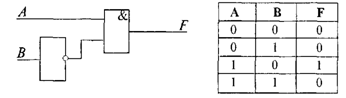
Заполненная таблица истинности полностью описывает рассматриваемую комбинационную схему. Другая форма описания логических устройств — структурная формула.
Пример 3. По заданной комбинационной схеме выпишем структурную формулу.

Пример 4. По структурной формуле вычертим соответствующую комбинационную схему:
Ú
Решение. Нам потребуются два инвертора, два конъюнктора и один дизъюнктор.


            5. Синтез комбинационных схем

Предположим, что имеется таблица истинности некоторой логической функции, где указывается, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах. Синтез произвольной комбинационной схемы по заданной таблице истинности заключается в получении структурной формулы, описывающей работу схемы, в упрощении этой формулы и в составлении искомой схемы по минимизированной формуле.
            Структурные формулы могут быть упрощены на основании законов алгебры логики. Эта работа требует большой аккуратности и внимания, так как даже малейшая неточность приводит к ошибочному результату.

Основным звеном проектирования логической схемы цифрового устройства является синтез

Пример 1. По заданной таблице истинности синтезировать комбинационную схему:

Решение.

1-й способ: F(A,B)_СДНФ =

2-й способ:
_СДНФÚÚÚÚ=
ÚÚÚÚÚÚÚÚ

Заметим, что запись СКНФ для этого примера сразу же дает нам нужный результат. Комбинационная схема имеет следующий вид.

            6. Примеры комбинационных схем

6.1. Сумматор

Сумматор – комбинационное устройство, обеспечивающее суммирование двоичных чисел. Рассмотрим схему сложения двух n-разрядных двоичных кодов.

+

При сложении цифр i-го разряда складываются а_i и b_i. Результатом будет с_i и p_i — перенос в старший разряд.

Таким образом, одноразрядный двоичный сумматор — это устройство с тремя входами и двумя выходами. Его работа может быть описана следующей таблицей истинности:

Ниже приведено условное обозначение сумматора:



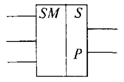
Если складывать n-разрядные двоичные слова, то можно использовать последовательное соединение таких сумматоров.

6.2. Триггер

Триггером называют узел, способный хранить один разряд двоичного числа. Самый простой триггер — RS. Он состоит из двух элементов ИЛИ—НЕ. Его схема и таблица истинности приведены ниже:

Входы Состояние Q R S 0 0 Q 0 1 1 1 0 0 1 1 Недопустимо

Обычно на входы поступают сигналы R = 0 и S = 0, и триггер хранит старое состояние. Если на вход S поступает на короткое время сигнал 1, то триггер переходит в состояние 1, и после того как сигнал S станет равен 0, он будет сохранять это состояние. При подаче 1 на вход R триггер перейдет в состояние 0. Подача на оба входа логической единицы может привести к неоднозначному результату, поэтому такая комбинация входных сигналов запрещена.

Для запоминания 1 байта информации необходимо 8 триггеров, для 1 Кбайта — 8—1024 триггера. Оперативная память
современных ЭВМ содержит миллионы триггеров.

В заключение отметим, что ЭВМ состоит из огромного числа отдельных логических элементов, образующих все ее узлы и память.

6.3. Дешифратор

Дешифратор— комбинационное устройство, преобразующее комбинацию входных переменных в активный сигнал только на одном из его выходов.

Максимальное количество выходов дешифратора равно 2ⁿ,
где n – число входов.


 Таблица истинности дешифратора

6.4. Шифратор

Шифратор (coder) — комбинационное устройство, выполняющее функцию, обратную по отношению к дешифратору,
т. е. формирование двоичного кода на выходах при появлении сигнала на одном из входов.


 Таблица истинности шифратора

Список рекомендуемой литературы

Е.В. Ширшов. Учебный практикум по вычислительной технике : метод. указания и задания к контрольным работам / Е.В. Ширшов О.В. Чурбанова. – Ростов н/Д : Феникс, 2006. – 256 с.

Калиш Г.Г. Основы вычислительной техники : учеб. пособие / Г.Г. Калиш. – М. : Высш шк., 2000. – 271 с.

Кузин А.В. Микропроцессорная техника : учебник для сред. проф. образования / А.В. Кузин, М.А. Жаворонков. – М. : Академия, 2004. – 304 с.