Реферат по математическому анализу на тему:
«Элементарные функции и их свойства»
Оглавление
I.Введение.3
II.Элементарные функции.4
1. Элементарные функции по Лиувиллю.. 4
2. Многочлен.. 5
3. Полиномиальные функции.6
4. Рациональная функция. 7
5.Степенная функция. 7
6.Показательная функция. 8
7.Логарифм.. 10
8.Тригонометрические функции. 11
9.Обратные тригонометрические функции.. 14
III.Заключение.21
IV.Список литературы.21
I. Введение.
Термин «функция» появился в одной работе Лейбница в 1692г., а затем применялся братьями Якобом и Иоганном Бернулли для характеристики различных отрезков, так или иначе связанных с точками некоторой кривой. В 1718г. Иоганн Бернулли впервые даёт определение функции, свободное от геометрических представлений. Его ученик Эйлер в своём учебнике « Введение в анализ бесконечно малых» воспроизводит определение Бернулли, несколько его уточняя:
«Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и из чисел или постоянных количеств».
В течение ряда десятилетий существенного прогресса в определении понятия функции не было. Обычно приписывают Дирихле заслугу выдвижения на первый план идеи соответствия, которая лежит в основе этого понятия.
Задачи:
Ø Узнать, какие функции можно получить из основных элементарных функций;
Ø Узнать, какими свойствами обладают основные элементарные функции.
Цель:
ü Расширение кругозора своих знаний об основных элементарных функциях.
II. Элементарные функции.
Элементарные функции — функции, которые можно получить из основных элементарных функций:
- Полиномиальная функция,
- рациональная,
- степенная,
- показательная и логарифмическая,
- тригонометрические и обратные тригонометрические
с помощью конечного числа арифметических действий и композиций. Каждую элементарную функцию можно задать формулой, т.е. набором конечного числа символов, отвечающих перечисленным операциям.
1. Элементарные функции по Лиувиллю.
Рассматривая функции комплексного переменного, Лиувилль определил элементарные функции несколько шире. Элементарная функция y переменной x — аналитическая функция, которая может быть представлена как алгебраическая функция  от x и функций
от x и функций  , причем
, причем  является логарифмом или экспонентой от некоторой алгебраической функции g1 от x.
является логарифмом или экспонентой от некоторой алгебраической функции g1 от x.
Например, sin(x) — алгебраическая функция от eix.
Не ограничивая общности рассмотрения, можно считать функции  алгебраически независимы, то есть если алгебраическое уравнение
алгебраически независимы, то есть если алгебраическое уравнение  выполняется для всех x, то все коэффициенты полинома
выполняется для всех x, то все коэффициенты полинома  равны нулю.
равны нулю.
2. Многочлен.
В математике, многочлены или полиномы от одной переменной

где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.
Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.
Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.
Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.
3. Полиномиальные функции.
Пусть A есть алгебра над кольцом R. Произвольный многочлен  определяет полиномиальную функцию
определяет полиномиальную функцию
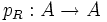 .
.
Чаще всего рассматривают случай A = R.
В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция  полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены
полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены  и
и  из
из  определяют тождественно равные функции
определяют тождественно равные функции  .
.
Свойства:
- Кольцо многочленов над произвольной областью целостности само является областью целостности.
- Кольцо многочленов от любого конечного числа переменных над любым факториальным кольцом само является факториальным.
- Кольцо многочленов от одного переменного над полем является кольцом главных идеалов, т. е. любой его идеал может быть порожден одним элементом.
- Более того, кольцо многочленов от одного переменного над полем является евклидовым кольцом.
4. Рациональная функция.
Текущая версия (не проверялась)
Функция называется рациональной, если она может быть представлена в виде дроби:

где  ,
,  — многочлены.
— многочлены.
Такая функция определена во всех точках, кроме тех, в которых знаменатель  обращается в ноль.
обращается в ноль.
Свойства:
- Любое выражение, которое можно получить из переменных
 с помощью четырёх арифметических действий, является рациональной функцией.
с помощью четырёх арифметических действий, является рациональной функцией. - Множество рациональных функций замкнуто относительно арифметических действий и операции композиции.
- Любая рациональная функция может быть представлена в виде суммы простейших дробей (см. Метод неопределённых коэффициентов), это применяется при аналитическом интегрировании.
5. Степенная функция.
Степенная функция комплексного переменного f(z) = zn с целочисленным показателем определяется с помощью аналитического продолжения аналогичной функции вещественного аргумента. Для этого применяется показательная форма записи комплексных чисел.
А именно, известно, что любое комплексное число может быть представлено через его модуль и аргумент с помощью формулы Эйлера в виде z = | z | eiargz. Пользуясь этим, запишем пока формальное выражение для степенной функции:

6. Показательная функция.
Показательная функция — функция обычно обозначаемая ax, где a — некоторое вещественное число, а x — переменная. Если в качестве a (называемого также основанием) стоит число e, то функция называется экспонентой.
 |
Свойства:
Опишем свойства введённой нами функции.
1). a(x+y) = a(x)a(y). Для доказательства этого факта докажем сперва лемму: если 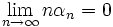 , то
, то  .
.
При достаточно больших n |αn| становится меньше единицы; по неравенству Бернулли получаем, что  =
=  . Видим, что самая левая и самая правая части стремятся к единице, а значит, по теореме о неравенстве пределов, и заключённое между ними выражение стремится к тому же числу, ч. т. д.
. Видим, что самая левая и самая правая части стремятся к единице, а значит, по теореме о неравенстве пределов, и заключённое между ними выражение стремится к тому же числу, ч. т. д.
Теперь доказательство собственно свойства. a(x)a(y) =  =
=  =
=  =
=  =
=  , где α =
, где α =  . Из этого свойства следует, что a(x)a(-x)=1.
. Из этого свойства следует, что a(x)a(-x)=1.
2). Из свойства 1 следует, что для любого x a(x) неотрицательна, но a(x) = a(x/2+x/2) = a(x/2)², а значит, a(x) всегда положительна.
3). a(x) возрастает. Действительно, если x2 > x1, то a(x2) = a(x1 + (x2 — x1)) = a(x1)a(x2 — x1), где a(x1) положительно, а следующий сомножитель больше единицы (так как, по всё тому же неравенству Бернулли, a(x) >= 1+x).
4). a(x) непрерывна. Докажем непрерывность в нуле: 1+x  , а значит, предел в нуле равен единице — значению в нуле. Если мы рассмотрим x0, то увидим, что a(x) = a(x0)a(x-x0), при стремлении x к x0 правый множитель стремится к 1, поэтому предел a(x) в точке равен значению её в этой же точке, ч. т. д.
, а значит, предел в нуле равен единице — значению в нуле. Если мы рассмотрим x0, то увидим, что a(x) = a(x0)a(x-x0), при стремлении x к x0 правый множитель стремится к 1, поэтому предел a(x) в точке равен значению её в этой же точке, ч. т. д.
7. Логарифм.

Логарифм числа a по основанию b равен показателю степени, в которую надо возвести число b, чтобы получить число a (если  , то
, то  , где b>0 и b≠1, a>0). Широкое применение нашли логарифмы по основаниям e (число Эйлера) — натуральные логарифмы (
, где b>0 и b≠1, a>0). Широкое применение нашли логарифмы по основаниям e (число Эйлера) — натуральные логарифмы (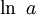 ) и по основанию 10 — десятичные логарифмы (
) и по основанию 10 — десятичные логарифмы ( ), а также двоичные логарифмы (
), а также двоичные логарифмы ( ,
,  ), которые применяются в теории информации и информатике.
), которые применяются в теории информации и информатике.
Основные свойства:
8. Тригонометрические функции.


Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометри́ческие фу́нкции — математические функции от угла. Они важны при изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. Более современные определения выражают тригонометрические функции через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций даже на комплексные числа.
| Основные тригонометрические функции: | ||
| Функция | Обозначение | Соотношение |
| Си́нус | sin |
|
| Ко́синус | cos |
|
| Та́нгенс |
|
|
| Кота́нгенс |
|
|
| Се́канс | sec |
|
| Косе́канс |
|
|
Свойства тригонометрических функций:
Функция y = cos x — чётная. Функции: y = sin x, y = tg x, y = ctg x — нечётные, то есть:




Для острых углов  справедливо:
справедливо:




Для углов  справедливо:
справедливо:



История.
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
9. Обратные тригонометрические функции.
Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными[источник?] к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:
- аркси́нус (обозначение: arcsin)
- аркко́синус (обозначение: arccos)
- аркта́нгенс (обозначение: arctg; в иностранной литературе arctan)
- арккота́нгенс (обозначение: arcctg; в иностранной литературе arccot или arccotan)
- арксе́канс (обозначение: arcsec)
- арккосе́канс (обозначение: arccosec; в иностранной литературе arccsc)
Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arc — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin−1 для арксинуса и т.п.; это считается неоправданным, так как возможна путаница с возведением функции в степень −1.
Функция arcsin.


График функции y = arcsinx.
Арксинусом числа m называется такой угол x, для которого 
Свойства функции arcsin:
 (функция является нечётной).
(функция является нечётной). при
при 
 при x = 0.
при x = 0.  при
при 


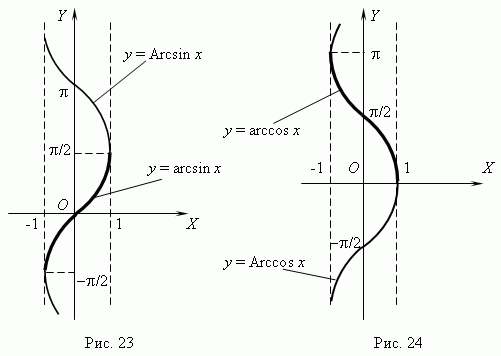
Функция arcos.


График функции y = arccosx.
Арккосинусом числа m называется такой угол x, для которого 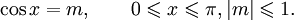
Свойства функции arcos:
- arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки

- arccosx > 0 при

- arccosx = 0 при x = 1.


Формула выше, по-моему, не очень верна [xmode]

Функция arctg.


График функции  .
.
Арктангенсом числа m называется такой угол x, для которого 
Свойства функции arctg:
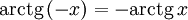 (функция нечётная).
(функция нечётная).  при x > 0.
при x > 0.  при x = 0.
при x = 0.  при x < 0.
при x < 0. 

Функция arcctg.


График функции y=arcctg x
Арккотангенсом числа m называется такой угол x, для которого 
Свойства функции arcctg:
 (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 
 при любых x.
при любых x. 
Использование в геометрии:


Прямоугольный треугольник ABC
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.
В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол:
α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a) .
III. Заключение.
Изучением функций, в частности, элементарных, занимались многие ученые-математики на протяжении всего развития функций, но и сейчас нельзя сказать, что они полностью и подробно изучены, и я попыталась расширить кругозор своих знаний об элементарных функциях, я узнал какие функции можно получить из основных элементарных функций, и какими свойствами они обладают.
IV. Список литературы.
1. Н.С. Пискунов «Дифференциальное и интегральное исчисления», том первый, М, «Интеграл-пресс», 2002.
2. Г.М. Фихтенгольц «Основы математического анализа», часть 1, М, «Лань», 2002.
3. Свободная электронная энциклопедия «Википедия».























 или tan
или tan
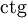 или cot
или cot

 или csc
или csc
 (zip - application/zip)
(zip - application/zip)










