Уравнение распространения тепла в стержне

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ  АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ  УНИВЕРСИТЕТ

Кафедра  «Промышленная теплоэнергетика»

Реферат по дисциплине «Уравнения математической физики в процессах тепломассообмена»

 на тему:

«Уравнение распространения тепла в стержне»

                                                                       Выполнил: ст. гр.ПТм-15-1

                                                                                
          Жаровцев Р.Д.

                                                                              Проверила: доцент

Лободенко Е.И.

Тюмень 2016г.

Оглавление

Введение. 3

1 Уравнения в частных производных. 3

2 Распространение тепла в стержне. 4

3 Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне. 6

4 Решение задачи спектральным методом.. 11

Заключение. 15

Список источников. 16

Введение

В данной работе рассматриваются методы решения уравнения распространения тепла в стержне. В первой части работы рассматриваются уравнения в частных производных. Эти уравнения называются основными уравнениями математической физики. Они описывают физические процессы, относящиеся к области механики сплошных сред. Именно этим и объясняется название курса "Уравнения математической физики".  Во второй части речь идет об основных уравнениях математической физики полученных на основе общих законов физики, описывающие распространение тепла в стержне. Далее, более подробно, рассматривается метод Фурье для одномерного уравнения теплопроводности, так же известный как метод разделения переменных. В заключительной части работы описывается спектральный способ решения данной задачи, с использованием программного обеспечения Matlab/Octave.

 1 Уравнения в частных производных

Уравнением с частными производными относительно функции u(x₁,…,x_n) называется уравнение, содержащее хотя бы одну из частных производных этой функции. Порядком уравнения с частными производными называется порядок наивысшей производной входящей в это уравнение. Дифференциальное уравнение с частными  производными называется линейным, если искомая функция и ее частные производные входят в него линейно (т.е. в первой степени) [1] 

   Решение уравнения в частных производных может содержать произвольные функции, в отличие от обыкновенных дифференциальных уравнений, решение которых может содержать лишь произвольные постоянные.

Пример.

              Очевидно, что функция  U(x,y) = j(y) есть решение уравнения , где  j(y) произвольная функция от y.

   Наибольший практический интерес представляют дифференциальные уравнения  второго порядка. В частности, линейное уравнение с частными производными второго порядка с искомой функцией U(x,x,…,x) от n независимых переменных имеет вид:

          (1)

где a_i,j = a_j,i , i,j =1,2,…,n .    a_i,j, b_i, c, f – есть функции x₁,x₂,…,x_n.

  Если f(x_1,x₂,...,x_n) = 0, то уравнение (1) называется линейным однородным уравнением, в противном случае - линейным неоднородным.

   Среди уравнений с частными производными второго порядка следует выделить три типа, которые для функций двух независимых переменных имеют

вид.

Волновое уравнение (уравнение гиперболического типа)	(2)
Уравнение теплопроводности или уравнение Фурье (уравнение параболического типа)	(3)
Уравнение Лапласа (уравнение эллиптического вида)	(4)

2 Распространение тепла в стержне

Основные уравнения математической физики получены на основе общих законов физики. Получим уравнение теплопроводности, рассматривая процесс теплопередачи в однородном ограниченном стержне длиной l. Будем считать,

0                       x₁                  x₂                                                                                
  l

что боковая поверхность теплоизолирована, а температура в поперечном сечении одинакова. Один конец стержня расположен в точке x = 0, тогда другой конец будет иметь координату x = l.

   Пусть T(x,t) - температура в точке x в момент времени t.

   Скорость распространения тепла (количество тепла протекающего через поперечное сечение стержня с абсциссой x за единицу времени) установлена опытным путем:    

                                               S - площадь сечения стержня;

                                                                      λ-коэффициент теплопроводности.   

     Рассмотрим элемент стержня, заключенный между сечениями с абсциссой x₁ и x₂. Обозначим   Dx = x₂ – x₁. Через сечение с абсциссой x₁ за время  Dt пройдет количество тепла равное  .

То же самое, для сечения с абсциссой x₂:   ,

 где  означает  при x = x_1, а   производная  при x = x₂.

   Приток тепла в рассматриваемый элемент стержня за время Dt будет:

            [] – [ ] @ l         (5)

В выражении (5) применена теорема Лагранжа .

В результате этого притока тепла температура в рассматриваемом элементе стержня изменяется на величину DT, т.е.

                                                                       DQ₁ -DQ₂  = С× r×Dx×S×DT

или                                                       DQ₁ -DQ₂  @ С× r×Dx×S×                   (6)

где С – теплоемкость вещества стержня;

      r - плотность вещества стержня.

Приравнивая (5) и (6) получим: l  = С× r×Dx×S×

Или    = .         Обозначим             

   Уравнение теплопроводности в стержне примет вид:

                                                                                           (7)

Это простейшее уравнение параболического типа.

   Рассматривая процесс распространения тепла в 3-х мерном пространстве, где температура Т(x,y,z,t) является функцией координат (x,y,z) и времени t, можно получить уравнение теплопроводности  в виде:

                                                                    (8)

Если функция Т(x,y,z,t) не зависит от z, т.е. температура не зависит от z, то получим уравнение распространения тепла на плоскости:

                                          = a² (+).                                    (9)

Коэффициент a² имеет тот же смысл что и в уравнении (7).

3 Метод Фурье для одномерного уравнения теплопроводности. Распространение тепла в ограниченном стержне

Рассмотрим задачу о распространении тепла в стержне, концы которого поддерживаются при нулевой температуре. Стержень считаем однородным и тонким, так, что d<, где ось  направлена вдоль стержня. Боковая поверхность стержня предполагается изолированной от окружающей среды.

В начальный момент времени  задано распределение температуры вдоль стержня, характеризуемое  функцией . Указан также тепловой режим, поддерживаемый на концах стержня – считаем температуру на его концах равной нулю. Задача состоит в отыскании решения уравнения теплопроводности

,  , (10)

при граничных условиях

,   (11)

и при начальном условии

, (12)

где  – непрерывна, имеет кусочно-непрерывную производную и удовлетворяет условиям согласования с требованиями (11) 

Метод разделения переменных, называемый также методом Фурье, заключается в следующем:

1. Ищем частные решения уравнения (10) в виде 

 . (13)

2. Подставляя (13) в (10) получаем уравнение 

.

Разделив обе части полученного уравнения на  из (13), имеем

 . (14)

Постоянная , называемая постоянной разделения, появилась в (14) из следующих соображений: левая часть в (14) зависит только от переменной , правая – только от переменной , и эти части должны быть равны при всех значениях   и . Поэтому оба отношения в (14) равны постоянной. Приравнивая каждое отношение в (14) постоянной, получим два обыкновенных дифференциальных уравнения для функций  и :

  (15)

 (16)

3. По условию задачи функция  должна удовлетворять краевым условиям вида (16). Из (18) и (16) получаем условия для функции 

,  .

Таким образом, для функции  получили задачу: требуется найти не равные тождественно нулю решения краевой задачи

  , , (15’)

а также числовые значения параметра, при которых существуют ненулевые решения задачи (15), (15’).

Поставленная задача называется задачей Штурма-Лиувилля. Указанные числовые значения  называются собственными значениями (числами) краевой задачи, соответствующие этим λ ненулевые решения – собственными функциями.

Найдем собственные числа краевой задачи (15), (15’). Рассмотрим возможности:

   

Пусть . Тогда общим решением уравнения (15) будет являться функция

.

При  и , имеем

 , , 

Следовательно, , поэтому  и начальное условие (12) не будет выполняться.

Пусть . Тогда общее решение уравнения (15) имеет вид

.

При   и , имеем

,  

систему двух однородных алгебраических уравнений, определитель которой не равен нулю. Поэтому , . И в этом случае условие (17) не удовлетворено.

Рассмотрим случай . В этом случае корни характеристического уравнения, соответствующего уравнению (15), равны , т.е. мнимые числа.

Как известно из курса теории дифференциальных уравнений, общее решение уравнения (15) имеет вид

.  (17)

При  получаем . При  имеем

,  , , (18)

где  . Подставляя (18) в (17), получаем

.  (19)

Входящие в формулу (19) функция и постоянная снабжены индексом, поскольку их значения зависят от .

Формула (18) определяет собственные числа, а формула (19) – собственные функции краевой задачи, соответствующие этим собственным числам.

4. Подставляя в уравнение (16) вместо  собственное значение  для определения функции , соответствующей данному собственному значению, получаем уравнение

  (20)

Общее решение уравнения имеет вид

  , (21)

где  - произвольные постоянные.

Итак, все функции

  (22)

удовлетворяют уравнению теплопроводности (10) и граничным условиям (11) при любых значениях  и любых постоянных . Но начальному условию (12) функции (22) в общем случае не удовлетворяют.

5. Требуем, чтобы решение удовлетворяло начальному условию (12). Для этого, учитывая (22), составим ряд

 . (23)

Каждый член этого ряда удовлетворяет уравнению (10) и краевым условиям (11).

Предположим, что функция  разлагается в равномерно и абсолютно сходящийся ряд Фурье. В силу начального условия, полагая в (23) , получаем

.  (24)

Написанный ряд представляет собой разложение функции  в ряд Фурье по синусам в промежутке (0,l). Коэффициенты  находятся по формуле

  . (25)

Предполагая, что  непрерывна, имеет кусочно-непрерывную производную и обращается в нуль при  и , получаем, что ряд (24) с коэффициентами (25) равномерно и абсолютно сходится к  (это известно из теории тригонометрических рядов).

Поскольку при  справедливы неравенства

 ,

то ряд (23) при  также сходится абсолютно и равномерно. Поэтому функция  (23) непрерывна при ,   и удовлетворяет начальному и граничному условиям.

Можно показать (мы не останавливаемся на этом), что функция  удовлетворяет уравнению (10) и имеет непрерывные производные по  и  первого и второго порядков соответственно [2]

4 Решение задачи спектральным методом

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:





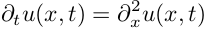
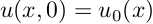
Такое уравнение решается аналитически методом разделения переменных, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:



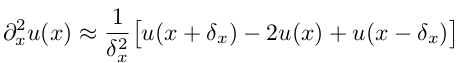
Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:



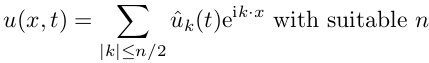
Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:





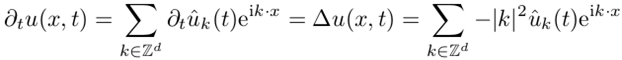
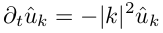
Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1)   в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;

2) разбиваем стержень на сетку из n точек;

3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);

4) умножаем полученные коэффиценты на -|k|², получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik)^p;

5) делаем обратное преобразование Фурье F^-1(u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;

6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо). 

Код для одномерного уравнения переноса тепла

clear all;

n = 50;             % number of points

dx = 2*pi/n;        % space step

x = 0:dx:2*pi-dx;   % grid

 

h = 0.1;            % temporal step

times = 10;         % number of iterations in time

 

k = fftshift(-n/2:1:n/2-1); % wave numbers

k2 = k.*k;            

 

u0 = 2 + sin(x) + sin(2*x); % initial conditions

u = zeros(times,n);         % stores results

u(1,:) = u0;

 

uf = fft(u0);                  % Fourier coefficients of initial function

 

for i=2:times

    uf = uf.*(1-h*k2);      % next time step in Fourier space

    u(i,:) = real(ifft(uf));  % IFFT to physical space

end

 

[X,T] = meshgrid(x,0:h:times*h-h);

waterfall(X,T,u)

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…



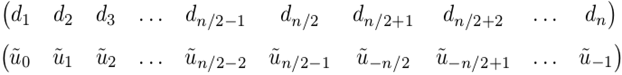
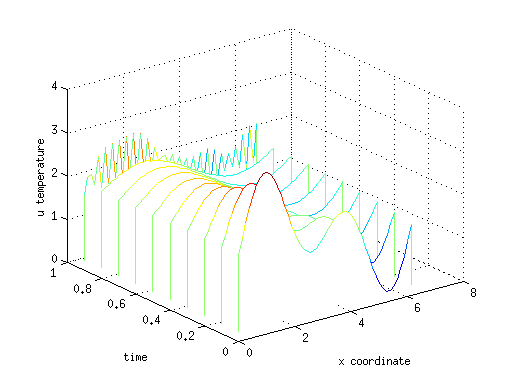
Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона [3]

Заключение

В данной работе рассматриваются методы решения одной из базовых задач, рассматриваемых в курсе математической физики, использующих уравнения распространения тепла в стержне. В применении к уравнениям в частных производных схема разделения переменных приводит к нахождению решения в виде ряда или интеграла Фурье. В этом случае метод также называют методом Фурье (в честь Жана Батиста Фурье, построившего решения уравнения теплопроводности в виде тригонометрических рядов) и методом стоячих волн.

В работе рассматриваются как аналитический метод решения, где результат выводится при помощи математических преобразований, так и численный метод, при котором результат соответствует действительному с заданной точностью, но который требует много рутинных вычислений и поэтому выполним только при помощи вычислительной техники (ЭВМ). В качестве числового расчета на ЭВМ в работе рассматривается так называемый спектральный метод, использующий программу Mathlab.

Основная суть спектрального метода, это замена исходных дифференциальных уравнений в частных производных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро. Спектральный метод эффективен в отношении памяти, поэтому широко используется в геофизике, моделировании климата и метеорологии.

 
Список источников

1. Лободенко Е.И., Курс лекции «Уравнения математической физики»
2. http://x-hunt.ru/zadasha/algebra37.html «Введение в математический анализ». Информационный портал.
3. https://habrahabr.ru/post/267401/  Информационный портал для IT специалистов. Статья «Спектральный метод на основе простых задач матфизики»
4. Сабитов, К.Б. Уравнения математической физики // Москва: Физматлит. – 2013