Федеральное агентство по образованию
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Хакасский Государственный Университет
Имени Н. Ф. Катанова
Кафедра математики и методики преподавания математики
РЕФЕРАТ
на тему:
Корни многочлена. Теорема Безу
Выполнили:
Студенты 1 курса группы ИМ-11
Очного отделения
Шабунин Дмитрий Олегович
Зорин Александр Сергеевич
Проверила:
Бобылева Оксана Владимировна
подпись___________________
Абакан
2016г.
План
Введение……………………………………………………………………………...3
1.Многочлены………………………………………………………………………..3
1.1.Определение многочлена………………………………………………………3
1.2.Определение корня многочлена……………………………………………….4
1.3.Схема Горнера………………………………………………………………….5
1.4.Нахождение корней по схеме Горнера. Виды корней……………………….7
2. Этьен Безу. Биография. Теорема Безу. Следствия из теоремы……………….13
2.1. Этьен Безу. Биогафия………………………………………………………...13
2.2. Теорема Безу………………………………………………………………….13
2.3 Следствия из теоремы Безу…………………………………………………..14
2.4. Примеры использования теоремы…………………………………………..14
Заключение………………………………………………………………………….16
Список используемых источников………………………………………………..17
ВВЕДЕНИЕ
Тема данного реферата: «Корни многочлена. Теорема Безу».
В нем мы хотим рассмотреть, что такое многочлен, что является корнем многочлена, а также рассказать про схему Горнера и теорему Безу.
В первой части мы разберем понятие многочлена, его корней и их виды и про схему Горнера. Во второй про теорему Безу.
Данная тема довольно актуальна, поскольку теорема Безу является одной из базовых теорем алгебры.
1. Многочлены
1.1. Понятие многочлена
Многочлен (полином) от одной переменной x – это выражение вида


 ,
,
где x – переменная , – коэффициенты из некоторого числового поля, n – целое
неотрицательное число, а нулевое- свободный член. Отдельные слагаемые вида ……, k=0,1,
…,n называются членами многочлена.
– коэффициенты из некоторого числового поля, n – целое
неотрицательное число, а нулевое- свободный член. Отдельные слагаемые вида ……, k=0,1,
…,n называются членами многочлена.
Также многочлен называют «полиномом», этот термин происходит от греческих слов «πολι» - много и «νομχ» - член.
2 члена называются подобными, если их степени равны. При этом подобные между собой члены можно преобразовать в один, т.е. привести подобные члены.
Степенью многочлена называют наибольшую среди степеней многочлена, при этом многочлен f(x)- не тождественный нуль. Обозначается эта степень deg(f).
Например:
 -многочлен четвертой степени (старшая
степень равна четырем);
-многочлен четвертой степени (старшая
степень равна четырем);
 - многочлен второй степени или квадратный (старшая
степень равна двум).
- многочлен второй степени или квадратный (старшая
степень равна двум).
При этом тождественный нуль степени не имеет.
Предполагается,
что коэффициенты многочлена принадлежат определенному полю (полю
действительных, рациональных, комплексных чисел). Так, если выполнять над
многочленом операции сложения, умножения или вычитания при помощи
сочетательного, переместительного и распределительных законов, мы получаем
снова многочлен.
Из
вышесказанного следует, что совокупность всех многочленов с коэффициентами из
данного поля Р образует кольцо Р - кольцо
многочленов над данным полем, это кольцо не имеет делителей нуля, т.е.
произведение многочленов, не равных нулю, не может дать нуль.
- кольцо
многочленов над данным полем, это кольцо не имеет делителей нуля, т.е.
произведение многочленов, не равных нулю, не может дать нуль.
1.2. Определение корня многочлена
Элемент
 кольца Р называется корнем многочлена f(x) ∈ Р
кольца Р называется корнем многочлена f(x) ∈ Р , если f(
, если f( )=0.
)=0.  Другими словами, число
Другими словами, число  является корнем многочлена f(x),
если в выражение
является корнем многочлена f(x),
если в выражение
 +
+ =0
=0
мы подставим  , тогда получим
, тогда получим
 +
+ =0.
=0.
Таким
образом, при подстановке вместо  число
число  получается верное выражение. Это означает, что число
получается верное выражение. Это означает, что число  является корнем равенства f(x)=0.
является корнем равенства f(x)=0.
Поэтому корень многочлена f(x) и корень соответствующего уравнения f(x)=0 по сути одно и то же.
К
примеру, найдём корень многочлена f(x)=3 -10+3
-10+3
Данное выражение является квадратным поэтому для нахождения корня многочлена нам необходимо решить следующее уравнение
3 -10х+3=0.
-10х+3=0.
Для этого необходимо рассмотреть алгоритм решения квадратных уравнений.
Алгоритм решения квадратных уравнений
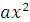 +bx+c=0
+bx+c=0
1.Найти
дискриминант D по формуле D= -4ac.
-4ac.
2.Если D<0, то квадратное уравнение не имеет корней.
3.Если D=0, то уравнение имеет один корень:

4.Если D>0, то уравнение имеет два корня:
 ,
,  .
.
Теперь
приступим к решению нашего уравнения 3 -10х+3=0,
-10х+3=0,
где  =3, b=-10 а с=3.
=3, b=-10 а с=3.
Находим дискриминант:
D= -4*3*3=64
-4*3*3=64
Поскольку D>0, то у данного уравнения два корня. Находим их:
 ;
;  .
.
Таким
образом, корнями многочлена f(x)=3 -10+3 будут
являться числа 3 и
-10+3 будут
являться числа 3 и  .
.
1.3.Схема Горнера
Схема
Горнера (или правило
Горнера, метод Горнера) — алгоритм вычисления значения многочлена,
записанного в виде суммы полиномов (одночленов), при заданном значении
переменной. Она, в свою очередь, и помогает нам выяснить, является ли
число  корнем данного многочлена или нет.
корнем данного многочлена или нет.
Для начала рассмотрим как делится многочлен f(x )на двучлен g(x).
Это можно записать следующим образом: f(x):g(x)=n(x), где f(x)- делимое, g(x)- делитель а n(x)- частное.
Но в случае, когда f(x) не делится нацело на g(x) имеет место общая запись выражения
 .
.
При
это степень r(x)< deg s(x), в таком
случае можно сказать, что  делится на
делится на  с остатком
с остатком  .
.
Рассмотрим деление многочлена на двучлен. Пусть
 ,
, 
 +...+
+...+ .
.
Получаем

Где r- число т.к. степень r должна быть меньше степени (x-c).
Умножим
s(x) на  и получим
и получим

Отсюда 
Таким образом, при делении на двучлен можно определять коэффициенты частного по полученным формулам. Подобный способ определения коэффициентов и называется схемой Горнера.
|
|
|
|
... |
|
|
|
+ |
|
|
... |
|
|
|
c |
|
|
|
... |
r |
Теперь рассмотрим несколько примеров применения схемы Горнера.
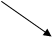
Пример. Выполнить деление многочлена f(x)= наx+3.
наx+3.
Решение. В начале необходимо записать (x+3) в виде (x-(-3)), поскольку в самой схеме будет участвовать именно -3.В верхней строке мы будем записывать коэффициенты, в нижней- результат действий.

 |
|||||||||
 |
 |
 |
 |
||||||
|
|
3 |
4 |
-5 |
-35 |
|
|
|
|
|
|
51 |
|
|
-3 |
1 |
3+(-3)=0 |
4 |
-17 |
16 |

 |










 По
полученным результатам запишем
По
полученным результатам запишем

Таким образом, мы получили f(x)= с остатком r(x)= 16.
с остатком r(x)= 16.
Пример. Выполнить деление многочлена f(x)= наx-2.
наx-2.
Решение.
|
1 |
4 |
-3 |
-2 |
|
|
+ |
2 |
12 |
18 |
|
|
2 |
1 |
6 |
9 |
16 |
f(x)=(x-2)(1 )+16.
)+16.
1.4.Нахождение корней по схеме Горнера. Виды корней
По схеме Горнера можно находить целочисленные корни многочлена f(x). Рассмотрим это на примере.
Пример. Найти все целочисленные корни
многочлена f(x)= , при помощи схемы Горнера.
, при помощи схемы Горнера.
Решение.
Коэффициенты данного многочлена-
целые числа. Коэффициент перед старшей степенью(в нашем случае перед  ) равен одному. Поэтому, целочисленные корни
многочлена мы будем искать среди делителей свободного члена (у нас это 15), это
числа:
) равен одному. Поэтому, целочисленные корни
многочлена мы будем искать среди делителей свободного члена (у нас это 15), это
числа:
Начнем проверку с числа 1.
Таблица №1
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
Из полученной таблицы видно, что при  =1 многочлен многочлена f(x)=
=1 многочлен многочлена f(x)=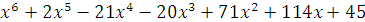 , мы получили остаток r=192, а не 0,
из этого следует, что единица не является корнем. Поэтому продолжим проверку
при
, мы получили остаток r=192, а не 0,
из этого следует, что единица не является корнем. Поэтому продолжим проверку
при  =-1. Для этого мы не будем создавать новую таблицу, а
продолжим в старой, а уже не нужные данные зачеркнем.
=-1. Для этого мы не будем создавать новую таблицу, а
продолжим в старой, а уже не нужные данные зачеркнем.
Таблица №2
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
 |
|
 |
Как
мы видим из таблицы, в последней ячейке получился нуль, а это значит, что r=0.
Следовательно? число -1 является корнем данного многочлена. Поделив наш
многочлен многочлена f(x)=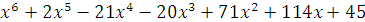 на (
на ( )=x+1 мы получили многочлен
)=x+1 мы получили многочлен
f(x)=(x+1)( ),
),
коэффициенты для которого мы взяли из третей стоки таблицы № 2.
Также мы можем сделать равносильную запись
 (x+1)(
(x+1)( ). Пометим его (1)
). Пометим его (1)
Теперь
необходимо продолжить поиск целочисленных корней, но только сейчас мы уже будем
искать корни многочлена  . Искать эти корни мы будем среди свободного члена
многочлена, числа 45.
. Искать эти корни мы будем среди свободного члена
многочлена, числа 45.
Еще раз проверим число -1.
Таблица №3
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
|
+ |
-1 |
0 |
22 |
-24 |
-45 |
||
|
-1 |
1 |
0 |
-22 |
24 |
45 |
0 |


Таким
образом, число -1 является корнем многочлена  , его можно записать в виде
, его можно записать в виде
 (2)
(2)
С учетом равенства (2) мы можем записать равенство (1) в следующем виде


 (3)
(3)
=

Теперь
ищем корни для многочлена  , опять же среди делителей свободного члена. Вновь
проверим число -1.
, опять же среди делителей свободного члена. Вновь
проверим число -1.
Таблица №4
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
|
+ |
-1 |
0 |
22 |
-24 |
-45 |
||
|
-1 |
1 |
0 |
-22 |
24 |
45 |
0 |
|
|
+ |
-1 |
1 |
21 |
-45 |
|||
|
-1 |
1 |
-1 |
-21 |
45 |
0 |
 |
|
 |
По
таблице мы видим, что число -1 является корнем многочлена  .
.
 (3*)
(3*)
С учетом (3*) мы можем переписать равенство (2*) как:
 (5)
(5)
Теперь
будем искать корень для  . Вновь смотрим делители свободного члена. Начнем
проверку вновь с числа -1.
. Вновь смотрим делители свободного члена. Начнем
проверку вновь с числа -1.
Таблица №5
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
|
+ |
-1 |
0 |
22 |
-24 |
-45 |
||
|
-1 |
1 |
0 |
-22 |
24 |
45 |
0 |
|
|
+ |
-1 |
1 |
21 |
-45 |
|||
|
-1 |
1 |
-1 |
-21 |
45 |
0 |
||
|
+ |
-1 |
2 |
19 |
||||
|
-1 |
1 |
-2 |
-19 |
64 |

 |
У
нас получился остаток не равный нулю, а это значит, что число -1 не является
корнем для многочлена . Проверим следующее число 1.
. Проверим следующее число 1.
Таблица №6
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
|
+ |
-1 |
0 |
22 |
-24 |
-45 |
||
|
-1 |
1 |
0 |
-22 |
24 |
45 |
0 |
|
|
+ |
-1 |
1 |
21 |
-45 |
|||
|
-1 |
1 |
-1 |
-21 |
45 |
0 |
||
|
+ |
-1 |
2 |
19 |
||||
|
-1 |
1 |
-2 |
-19 |
64 |
|||
|
+ |
1 |
0 |
-21 |
||||
|
1 |
1 |
0 |
-21 |
24 |
 |
|
 |
|
 |
|
 |
И мы видим, что опять не подходит, остаток r(x)= 24.Берем новое число.
Проверим число 3.
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
|
+ |
-1 |
0 |
22 |
-24 |
-45 |
||
|
-1 |
1 |
0 |
-22 |
24 |
45 |
0 |
|
|
+ |
-1 |
1 |
21 |
-45 |
|||
|
-1 |
1 |
-1 |
-21 |
45 |
0 |
||
|
+ |
-1 |
2 |
19 |
||||
|
-1 |
1 |
-2 |
-19 |
64 |
|||
|
+ |
1 |
0 |
-21 |
||||
|
1 |
1 |
0 |
-21 |
24 |
|||
|
+ |
3 |
6 |
-45 |
||||
|
3 |
1 |
2 |
-15 |
0 |





 Таблица №7
Таблица №7
r(x)= 0,
это значит, что число 3 является корнем многочлена  , этот многочлен мы можем записать как:
, этот многочлен мы можем записать как:
 =(x-3)(
=(x-3)( )
)
Учитывая получившееся выражение, мы можем записать равенство (5) в следующем виде:
 ( x-3)(
( x-3)( ) (6)
) (6)
Проверим
теперь для многочлена 
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
|
+ |
-1 |
0 |
22 |
-24 |
-45 |
||
|
-1 |
1 |
0 |
-22 |
24 |
45 |
0 |
|
|
+ |
-1 |
1 |
21 |
-45 |
|||
|
-1 |
1 |
-1 |
-21 |
45 |
0 |
||
|
+ |
-1 |
2 |
19 |
||||
|
-1 |
1 |
-2 |
-19 |
64 |
|||
|
+ |
1 |
0 |
-21 |
||||
|
1 |
1 |
0 |
-21 |
24 |
|||
|
+ |
3 |
6 |
-45 |
||||
|
3 |
1 |
2 |
-15 |
0 |
|||
|
+ |
3 |
15 |
|||||
|
3 |
1 |
5 |
0 |





 Таблица №8
Таблица №8
Исходя
из таблицы, мы видим, что число 3 это корень многочлена  . Теперь запишем следующее:
. Теперь запишем следующее:

Запишем равенство (5*), с учетом получившегося выражения, следующим образом:
 ( x-3)(
( x-3)( )=
)= =
= .
.
Найдем
корень для двучлена  среди делителей свободного члена.
среди делителей свободного члена.
Возьмем число 5
Таблица №9
|
1 |
2 |
-21 |
-20 |
71 |
114 |
45 |
|
|
+ |
1 |
3 |
-18 |
-38 |
33 |
147 |
|
|
1 |
1 |
3 |
-18 |
-38 |
33 |
147 |
192 |
|
+ |
-1 |
-1 |
22 |
-2 |
-69 |
-45 |
|
|
-1 |
1 |
1 |
-22 |
2 |
69 |
45 |
0 |
|
+ |
-1 |
0 |
22 |
-24 |
-45 |
||
|
-1 |
1 |
0 |
-22 |
24 |
45 |
0 |
|
|
+ |
-1 |
1 |
21 |
-45 |
|||
|
-1 |
1 |
-1 |
-21 |
45 |
0 |
||
|
+ |
-1 |
2 |
19 |
||||
|
-1 |
1 |
-2 |
-19 |
64 |
|||
|
+ |
1 |
0 |
-21 |
||||
|
1 |
1 |
0 |
-21 |
24 |
|||
|
+ |
3 |
6 |
-45 |
||||
|
3 |
1 |
2 |
-15 |
0 |
|||
|
+ |
3 |
15 |
|||||
|
3 |
1 |
5 |
0 |
||||
|
+ |
-5 |
||||||
|
-5 |
1 |
0 |
 |
|||
 |
|||
 |
|||
 |
|||
 |
|||
 |
r(x)=0,
следовательно, 5 является корнем двучлена .
.
Таким образом, мы можем записать
 .
.
Решением данного примера будет являться таблица№8.
Как видно из таблицы, числа -1;3;5 – корни многочлена.
Теперь перейдем непосредственно к видам корней.
-1- корень третьей степени, поскольку скобка (x+1) находится в третьей степени;
3- корень второй степени, скобка(x-3) во второй степени;
5- корень первой степени или, другими словами, простой.
2.Этьен Безу. Биография. Теорема Безу. Следствия из теоремы.
2. 1.Этьен Безу. Биография
Этьен Безу — французский математик, член Парижской Академии Наук (с 1758 года).
Родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года.
С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.
Основные работы Этьена Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.
В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения
неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную К. Маклореном) о том, что две кривые
порядка m и n пересекаются не более чем в m-nточках.
Безу писал “Курс математики" пять лет с 1764 по 1769 год. Также, он развил метод неопределённых множителей: в элементарной алгебре его
именем назван способ решения систем уравнений, основанный на этом методе.
Часть трудов Безу посвящена внешней
баллистике.
2.2. Теорема Безу.
Теорема Безу довольно просто в своем использовании, но при этом она является одной из базовых теорем теории многочлена. Она гласит, что остаток от деления многочлена f(x) на многочлен (x-c) - это f(c).
f(x) – многочлен с коэффициентами из кольца P.
Доказательство:
Раздели
многочлен f(x) на двучлен (x-c) с
остатком  . Получим
. Получим
 .
.
Теперь подставим в получившееся равенство вместо x число с. Получаем
 +r
+r
Так
как скобка  равна нулю, то из этого следует, что
равна нулю, то из этого следует, что
 r.
r.
Теорема
доказана.
2.3. Следствия из теоремы Безу.
Следствие 1. Число с - корень многочлена  тогда и только тогда, когда
тогда и только тогда, когда  делится без остатка на двучлен
делится без остатка на двучлен  .
.
Следствие 2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
Следствие 3. Пусть - целый корень многочлена
- целый корень многочлена с целыми коэффициентами. Тогда для любого
целого n число
с целыми коэффициентами. Тогда для любого
целого n число  делится на
делится на  .
.
Благодаря
данной теореме и ее следствия, мы можем, найдя один корень многочлена, искать
остальные корни многочлена, но степень которого будет на единицу ниже. Если , то многочлен
, то многочлен  будет выглядеть следующим образом
будет выглядеть следующим образом

Это
означает, что один корень уже найден. Дальше следует находить корни многочлена , степень которого на один ниже степени многочлена
, степень которого на один ниже степени многочлена 
Также данный метод называют понижением степени. Благодаря данному способу можно найти оставшиеся корни многочлена.
2.4. Примеры использования теоремы.
Пример.
Найти остаток от деления многочлена  на
на  .
.
Решение. На основании теоремы Безу подставляем вместо x число -5. Получаем
r(x)=
В результате мы получили остаток r(x) равный 180.
Пример.
С помощью теоремы Безу доказать, что
многочлен  делится на двучлен x-1 без остатка.
делится на двучлен x-1 без остатка.
Решение. Если данный многочлен  делится на двучлен x-1 без остатка, то, согласно теореме Безу, имеет место
равенство
делится на двучлен x-1 без остатка, то, согласно теореме Безу, имеет место
равенство  . Проверим.
. Проверим.

Что и требовалось доказать.
Пример.
Решить уравнение =0
=0
Решение. Целые корни многочлена должны быть делителями свободного члена, т.е. в нашем
случае, это делители числа три, так что это могут быть только числа
должны быть делителями свободного члена, т.е. в нашем
случае, это делители числа три, так что это могут быть только числа  При этом 1 не является корнем многочлена
При этом 1 не является корнем многочлена  , поскольку сумма его коэффициентов
, поскольку сумма его коэффициентов  .
.
При
 имеем схему:
имеем схему:
|
1 |
-1 |
-6 |
-1 |
3 |
|
-1 |
1 |
-2 |
-4 |
3 |
0 |
Мы
видим, что -1 – корень  , и в частном получается многочлен:
, и в частном получается многочлен:
 /
/
Значение
 второй раз проверять не будем, поскольку если бы число
1 было корнем
второй раз проверять не будем, поскольку если бы число
1 было корнем  то оно было бы и корнем
то оно было бы и корнем  , что неверно. Число -1 проверяем обязательно – ничто
не мешает ему быть также и корнем
, что неверно. Число -1 проверяем обязательно – ничто
не мешает ему быть также и корнем 
|
1 |
-2 |
-4 |
3 |
|
-1 |
1 |
-3 |
-1 |
4 |
Следовательно,
 0.
0.
Составим
схему Горнера для 
|
1 |
-2 |
-4 |
3 |
|
3 |
1 |
1 |
-1 |
0 |
Следовательно, , и при делении
, и при делении  на
на  получится многочлен
получится многочлен .
.
Таким
образом, многочлен  а значит и исходное уравнение, имеет 4 корня: -1, 3,
а значит и исходное уравнение, имеет 4 корня: -1, 3,  .
.
ЗАКЛЮЧЕНИЕ
Таким образом, мы рассмотрели понятие многочлена, что такое корни многочлена, схему Горнера, теорему Безу и ее следствия, которые помогают нам при решении задач, связанных с делимостью многочленов, например, нахождение остатка при делении многочленов, определение кратности многочленов и т.д. Также теорема работает при разложении многочленов на множители, при определении кратности корней и многих других.
Изучение
схемы Горнера и теоремы о рациональных корнях многочлена дает общий метод
разложения на множители любого алгебраического выражения. В свою очередь умение
решать уравнения высших степеней позволяет значительно расширить круг
показательных, логарифмических, тригонометрических и иррациональных уравнений и
неравенств.
В заключении, хотелось бы сказать что теорема Безу, не смотря на свою простоту, помогает при решении одной из главнейших задач математики- решения уравнений, т.е. нахождения его корней.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. . Е. В. Красова, О. В. Радченко Алгебра и теория чисел. Многочлены: учебно-методический комплекс по дисциплине: конспекты.– А.: ФГБОУ ВПО «Хакасский государственный университет им. Н. Ф. Катанова», 2012.- 68с.
2. Доктор физико-математических наук Глухов М. М., доктор физико-математических наук Родосский К.А., кандидат физико-математических наук Дорофеев Г. В. Алгебра многочленов: учебное пособие для студентов заочников III-IV курсов педагогических институтов М.: « Просвещение», 1980.-176с.
3. Бородин А.И., Бугай А.С.Биографический словарь деятелей в области— К.: Рад. школа, 1979.—607 с.
4. Автор не указан. Изучение теоремы Безу для решения уравнений n-й степени при n>2 // «Городская открытая научно-практическая конференция школьников и студентов». 2007.
5. http://www.calc.ru/Teorema-Bezu-Skhema-Gornera.html
6. http://math1.ru/education/raznoe/gorner.html
7. С. Каплунова Теория многочленов и уравнения высших степеней // Математика: учебно-методическая газета. —2007. — №14. — С.16-17















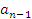


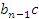





 1
1 +
+
 0
0 -12
-12 (zip - application/zip)
(zip - application/zip)










