Волновые свойства микрочастиц

 112

Глава 29. Волновые свойства микрочастиц

Из-за множителя а2 характерные для атома энергии на четыре порядкаменьше энергии покоя электрона. Это --- проявление нерелятивизмаатомной физики.

Задача 29.16. Определить скорость электрона на n-й орбите атома Бора.

Решение. Радиус n-й орбиты определяется формулой Rп = aBn 2, гдеаB --- радиус Бора. Скорость электрона V можно выразить через моментколичества движения L = пh:

                                                    

Выражение для радиуса Бора можно упростить, используя введенную

постоянную тонкой структуры:

                                      

Подставляя это выражение в полученную выше формулу для скоростиэлектрона, получаем для п---й орбиты:

                                                            

Отсюда вытекает, что на низшей орбите скорость электрона приблизи-тельно в 137 раз меньше скорости света, т.е. атом --- действительнонерелятивистская система. На n-й орбите скорости электрона в n разменьше, чем на первой. Численный пример: на второй орбите скоростьравна 2 =(2.998.108)/(2.137.036)=1.094 Мм/с ¦

При переходе с уровня k на уровень п (k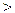п)излишек энергии Еk ---Еп перейдет в энергию фотона hvnk . Поэтому для спектра излучаемыхчастот получаем соотношение (ср. (29.1)):

29.5

                                     

                                                                                               

Таким образом, теория Бора позволила также вычислить постояннуюРидберга. Стало понятно и существование спектральных серий, и пре-дельные значения n,min (рис. 29.2).

Экспериментальное подтверждение гипотеза Бора нашла в опытахФранка-Герца: бомбардировка паров ртути электронами в вакуумной

29.1. Атом Бора

113

Рис. 29.2: Схема энергетических уровней в атоме Бора. Переходы электрона с высшего на низший уровень сопровождаются испусканием фотона, уносящего энергию, равную разности энергий уровней.

 трубке и измерение зависимости тока на коллекторе от ускоряющей раз-ности потенциалов. Чередование максимумов на равном расстоянии другот друга доказало дискретность изменения энергии атома.

Задача 29.17. При переходе с третьего уровня на второй (головная ли-ния серии Бальмера) водородоподобный ион атома некоего элемента ис-пускает фотон с энергией W = 7.5 эВ. Какой это элемент?

Решение. Энергия электрона, находящегося на п-й орбите вокруг ядрас зарядом Zе, равна

                                                    

При переходе с уровня га = 3 на уровень п = 2 выделяется энергия

                           

откуда

                                                    

Атомный номер элемента --- целое число, так что мы получили 2 = 2,что соответствует гелию. ¦

Еще до появления теории Бора был изучен спектр водородного атомаи эмпирически установлена формула . Но при наблюдении спектра

114

Глава 29. Волновые свойства микрочастиц

Солнца были замечены линии, казалось бы нарушающие эту формулу,т.к. они соответствовали полуцелым значениям п и к. После появлениятеории Бора стало ясно, что квантовые числа п и к все-таки должныбыть целыми, а кажущиеся полуцелые значения можно объяснить по-другому. Действительно, из формулы для частот, испускаемыхводородоподобным атомом, следует, что

                            

то есть наблюдавшиеся линии принадлежат иону элемента с Z = 2. Какизвестно, этот элемент носит ``солнечное"" имя --- гелий.

    • Волны материи

 Итак, снова дискретность, таинственные целые числа. В классическойфизике они появлялись в явлениях интерференции (номера максимумови минимумов) и в стоячих волнах (число узлов на закрепленных стру-нах). Луи де Бройль в 1923 г. выдвинул фундаментальную гипотезу:корпускулярно-волновой дуализм(с которым мы встретились на при-мере фотона) насамом деле присущ всем микрочастицам.Фотону мыбыли вынуждены приписать импульс р = h/.Долгое время уделялосьвнимание только его волновым свойствам, а в XX веке восстановили вправах и корпускулярные. С электроном получилось наоборот: лишь деБройль разглядел в нем колебания с длиной волны . Условие кван-тования Бора рR = пhполучило простую интерпретацию. Оно сталоусловием того, чтобы на длине стационарной орбиты уложилось целоечисло длин волн: 2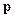R= п (аналогия с обоями: если по периметрукомнаты укладывается целое число периодов рисунка на обоях, то придальнейшем обклеивании рисунок воспроизводится на тех же местах ---своего рода стационарность). Отсюда вытекает соотношение  = h/р.Сравнивая с выражением , видим, что получилась общая формуладля фотонов и электронов (и любых других частиц).

Гипотеза де Бройля подтверждена экспериментами Дэвиссона и Джер-мера (отражение от кристаллических плоскостей) и Томсона (дифракцияна фольге). Красив и поучителен опыт В. А. Фабриканта (1949 г.) --- ди-фракция одиночных электронов, доказывающая, что волновые свойстваприсущи не коллективу электронов, но каждому в отдельности. И в тоже время электрон --- частица с зарядом и массой.

29.2. Волны материи

115

Вопрос, долго волновавший физиков: что такое микрочастица? Волнаили корпускула? Здесь налицо некорректная постановка вопроса, под-разумевающая альтернативу. Надо ``или"" заменить на ``и"": электрони волна, и частица. Если задать этот вопрос природе с помощью при-бора, то получим ответ, соответствующий прибору: для волнового при-бора (например, дифракционная решетка) ответ будет ``волна"", для кор-пускулярного (скажем, счетчик) --- ``частица"". Неоднозначность ответаотражает двойственность природы частиц или, точнее, узость нашегоальтернативного мышления, допускающего лишь одну из этих возмож-ностей. Это --- новые для нас объекты, квантовые русалки и кентаврымикромира, которых невозможно разделить на людей и животных. Вэтом смысле микрообъект --- ни волна, ни частица и ни их симбиоз. Это--- новое качество, которое мы количественно отражаем в формуле деБройля

                                                                                                                                 

связывающей волновые и корпускулярные проявления свойств единогообъекта. В экспериментах с ускоренными частицами их длина волныде Бройля играет ту же роль, что и длина волны видимого света, опре-деляющая разрешающую силу микроскопа. Ускорители --- своеобразныемикроскопы микромира, и с их помощью исследуются законы природы намалых расстояниях. Так, на ускорителе в Серпухове длина волны про-тонов составляет примерно 10-17 м, что в 10 млн раз меньше размероватомов.

При решении задач, связанных с длиной волны де Бройля, надо с осто-рожностью применять общую формулу  = h/р. Необходимо ясно пони-мать, какое выражение для импульса следует использовать. Например, взадаче может быть задана скорость частицы . Если эта скорость многоменьше скорости света с = 2.998 108 м/с, то можно применить класси-ческое соотношение р = тv. (На практике считают, что vс, еслиотношение v/c ? 0.3, т.е. v2/с2  0.1.) Если же это не так, то следуетприменить релятивистское соотношение между импульсом частицы иее скоростью:

                                                       

В задаче может быть задана не скорость частицы, а ее кинетическаяэнергия Еk. Критерием применимости классических формул являетсямалость кинетической энергии по сравнению с энергией покоя частицы

116

Глава 29. Волновые свойства микрочастиц

Ео = тс2.Если условие Ектс2 выполняется (что, как нетрудно ви-деть, эквивалентно условию vc ), то для нахождения импульса можновоспользоваться формулами классической механики

                                      

Если же кинетическая энергия частицы не мала по сравнению с энергиейпокоя (тем более, превышает ее), то следует использовать релятивист-ские формулы. В теории относительности выводится общее соотношениемежду полной энергией частицы Е и ее импульсом, которое уже встре-чалось выше :

 .

 Кинетическая энергия Ек равна разности между полной энергией и энер-гией покоя: Ек = Е --- тс2, так что для импульса получаем

                                                 

Наконец, удобно переписать это выражение так, чтобы под знаком ква-дратного корня стояли безразмерные величины:

                                               

Нетрудно убедиться, что при Ектс2 формула действительно пе-реходит в классическое выражение р =. Традиционные единицыэнергии (Дж) оказываются неудобными в микромире. Поэтому физикипредпочитают пользоваться несистемными единицами --- электронволь-том (эВ) и его производными (1 кэВ = 103 эВ, 1 МэВ = 10б эВ, 1 ГэВ =109 эВ и т.п.).

Электронвольт --- это энергия, приобретаемая электроном при прохо-ждении разности потенциалов 1 В: Е = еV. Так как заряд электронаравен е = 1.602 10-19 Кл, то 1 эВ = 1.602 10-19 Дж. Поскольку у наспоявилась энергия покоя, приведем ее численные значения для электронаи протона вместе с массами этих частиц. Заодно укажем численные зна-чения постоянной Планка, выраженной в эВ с:

h = 4.136 10-15 эВ с,

29.2. Волны материи

117

h = 6.582 10``16 эВ с,те= 9.109 10-31 кг,mес2 = 8.187 10-14 Дж = 0.511 МэВ,mр = 1.673 10-27 кг,

трс2 = 1.503 10-10 Дж = 938.3 МэВ.

Наконец, встречаются обратные задачи, когда задана длина волныде Бройля  и требуется найти скорость или энергию частицы. Встаетвопрос, как по величине  сразу определить, какими формулами сле-дует пользоваться. Представим себе, что мы применяем для нахожде-ния скорости классическую формулу р = тv и, следовательно, получаемv = h/т. Критерием справедливости этого результата является ма-лость v по сравнению с с:

                                                

Комбинации с = h/тси с = h/тс называются комптоновской дли-ной волны частицы. По своему физическому смыслу это --- характерноерасстояние, определяющее область, где уже неприменима нерелятивист-ская квантовая механика. Приведем численные значения этого важногопараметра для электрона и протона:

                           

  

 Видно, что чем легче частица, тем больше ее комптоновская длина волны,то есть тем раньше проявятся релятивистские эффекты. Для электронакомптоновская длина волны много меньше характерной длины, опреде-ляющей размеры атома. Это значит, что к атому применима нереляти-вистская квантовая механика. Ядра, состоящие из протонов и нейтронов,имеют размеры порядка 10-14 м, что много больше комптоновской длиныволны протона. Следовательно, к ним также применима эта теория.

Задача 29.18. Определить скорость частицы, у которой длина волныде Бройля в 10 раз меньше комптоновской длины волны с-

10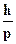

 Решение. По условию

 118

Глава 29. Волновые свойства микрочастиц

откуда находим для импульса частицы

р = 10mc.

Так как длина волны де Бройля меньше комптоновской длины волнычастицы, то мы не можем воспользоваться нерелятивистским соотно-шением р = те, которое приведет к несуразному ответу v = 10с (какизвестно, ничто не может двигаться быстрее света). Здесь необходимоприменить релятивистскую формулу связи импульса со скоростью:

                                                      

Отсюда вытекает уравнение

                                                      

решение которого дает

                                                   

то есть скорость частицы всего на 0.5% меньше скорости света. ¦

    • Соотношения неопределенностей

 Само наличие у частицы волновых свойств накладывает определенныеограничения на возможность корпускулярного описания ее поведения.Для классической частицы всегда можно указать ее точное положениеи импульс. Для квантового объекта имеем иную ситуацию.

Представим цуг волн пространственной протяженностью х --- образлокализованного электрона, положение которого известно с точностьюх . Длину волны электрона можно определить, подсчитав число пери-одов на отрезке: N= х /. Какова точность определения ? Ясно,что для слегка отличающейся длины волны мы получим то же самоезначение N. Неопределенность     

                                                                 

/2) в числе узлов, причем измерению доступны лишьN 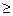 1. Так как р = h/ и р = h                  >    > >  E_ 1 E_ 2 

                                                                 

 влечет за собой неопределенность ее положения на орбитех = R  > 

                                                                 

) . Учитываясвязь момента количества движения Lс импульсом (L = Rр), получаемR = R р, откуда следует соотношение неопределенностей

L 

Для массивных объектов правая часть исчезающе мала, что позво-ляет одновременно измерить скорость и положение объекта (областьсправедливости классической механики). В атоме же Бора импульсэлектрона р= h/а, и неопределенность положения оказывается по-рядка размеров орбиты!

    • Невозможность достижения минимума потенциальной энергии. При-мер: осциллятор (тело на пружине):

                                                     

 Основное состояние в классической механике: р = 0 , х = 0 . Поэтомувеличина неопределенностей --- порядка самих импульса и коорди-нат:

                                            

 Минимум достигается в точке х =  и равен

                                                            

29.3. Соотношения неопределенностей

121

В принципе мы не можем претендовать на точный ответ, хотя в дан-ном случае (то же --- для атома водорода) он действительно точен.Мы получили так называемые нулевые колебания: квантовый осцил-лятор, в отличие от классического, не может оставаться в покое: этопротиворечит соотношению неопределенностей Гейзенберга. Точ-ные расчеты показывают, что формулу Планка для уровней энергииосциллятора надо было бы писать в виде

                                                                                     

При решении задач на применение соотношения неопределенностейследует иметь в виду, что в основном состоянии в классической фи-зике электрон покоится в точке, соответствующей минимуму потенци-альной энергии. Соотношения неопределенностей не позволяют ему этоделать в квантовой теории, так что электрон должен иметь некоторыйразброс импульсов. Поэтому неопределенность импульса (его отклонениеот классического значения 0) и сам импульс по порядку величины совпа-дают (р р).Неопределенность координаты электрона, замкнутого вобъеме V, равна по порядку величины линейному размеру этого объема

                                                           

Задача 29.19. Электрон с кинетической энергией 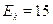 эВ находитсяна металлической пылинке диаметром d= 1 мкм. Оценить относитель-ную неточность v, с которой может быть определена скорость электрона.

Решение. По условию х? d/2и р?2h/d.Энергия электронамного меньше его энергии покоя, так что можно применять нереляти-вистские соотношения Ек = теv2/2, р=, р=mev,откуда v?2h/(теd). Для относительной неопределенности скоростиэлектрона получаем

                               

В этом выражении выделены безразмерные множители --- отношениекомптоновской длины волны электрона к диаметру пылинки и отноше-ние энергии покоя электрона к его кинетической энергии. Подставляемчисленные значения:

                                    

122

Глава 29. Волновые свойства микрочастиц

Задача 29.20. Среднее время жизни атома в возбужденном состоянии = 10-8 с. При переходе в основное состояние излучается фотон с длинойволны  = 0.5 мкм (зеленый цвет). Определить энергию кванта, ширинуи относительную ширину спектральной линии.

Решение. Энергия кванта равна

                             

Неопределенность в энергии определяется по соотношению t ):

                                  

 Отсюда

                                                 

                                     

    • О границах применимости квантовой механики

 Собственно, мы еще с квантовой механикой даже не познакомились, нолишь подошли к ее порогу. Тем не менее, уже сейчас можно дать оценкуобласти, в которой заведомо не будут справедливы выводимые нами со-отношения. Если подходить к микромиру со стороны области примени-мости классической физики, то никаких проблем не возникает. В самомделе, квантовые соотношения вовсе не отменяют классических законов,но уточняют их. В макромире с большими значениями энергий и мо-ментов количества движения квантовая дискретность просто будет неза-метна, так что спокойно можно применять и квантовые, и классическиезаконы. Разница между получаемыми с их помощью количественнымирезультатами будет ничтожно мала, но классические законы проще. Вэтом смысле мы говорим об области, где справедливы законы классиче-ской физики.

Иное дело, когда мы станем продвигаться вглубь микромира. В прин-ципе ясно, что где-то откажут и законы квантовой механики, и ученымпридется придумать какую-то новую теорию. В этом курсе мы будемзаниматься нерелятивистской квантовой механикой, изучающей микро-объекты, движущиеся со скоростями, гораздо меньшими скорости света

29.4. О границах применимости квантовой механики

123

с. Мы встретимся и с релятивистскими объектами (фотонами и др.), нобудем оговаривать такие случаи особо.

Определим теперь область справедливости нерелятивистской кванто-вой механики. Представим себе микрочастицу с массой т. Квантоваянеопределенность Е ее энергии должна быть много меньше энергиипокоя тс2 (в противном случае квантовые эффекты с необходимостьюбудут релятивистскими, что потребует обобщения теории). Из соотно-шения неопределенностей и условия применимости нерелятивист-ских уравнений Е  тс2 следует ограничение на интервалы времени:th/mc2. Характерное время tС = h/тс2 является, таким образом,водоразделом между релятивистской и нерелятивистской квантовыми те-ориями. За это время частица может пройти расстояние не большесtс = h/тс. Величина h/тс --- характерное расстояние, на которомпроходит граница между нерелятивистской и релятивистской теориями.Для электрона оно равно 3.86 10-13 м, а для протона --- 2.1 10" 16 м.Соответствующие промежутки времени равны tС = 1.3 10-21 с для элек-трона и tС= 7 10-25 с для протона.

На рис. 29.3 по оси х в логарифмическом масштабе отложены рассто-яния, а по оси у --- скорости. Отмечены области применимости основныхфизических теорий (ОТО --- общая теория относительности, СТО --- спе-циальная теория относительности, КТП --- квантовая теория поля, онаже --- релятивистская квантовая теория, она же --- теория элементарныхчастиц). Штриховкой показаны области применимости теорий, изучав-шихся нами. Правая граница заштрихованной области КМ не означает,что квантовую механику нельзя применять там, где мы привыкли поль-зоваться классической. Просто это делать нецелесообразно.

Обратим внимание, что рисунок ограничен с обеих сторон. Большойвзрыв, в котором родилась наша Вселенная, произошел 15-20 млрд леттому назад. За это время свет преодолел путь порядка 1026 м , что и опре-деляет максимальные возможные расстояния в этом мире. На расстоя-ниях порядка 10-35 м необходимо учитывать силы гравитации, квантоваятеория которых пока не создана. Только очень смелые теоретики реша-ются серьезно обсуждать, что происходит на столь малых расстояниях.Поэтому данная область на рисунке не показана.

Подведем итоги этой главы. Мы пришли к противоречивой картинемикромира. В атоме Бора использовались законы движения по класси-ческой траектории, которые в результате оказались несправедливыми.

 Глава 29. Волновые свойства микрочастиц

Рис. 29.3: Диаграмма расстояние-скорость делает наглядными области применимо-сти физических теорий: классической механики, специальной теории относительности(СТО), квантовой механики (КМ), общей теории относительности (ОТО) и квантовойтеории поля (КТП). Границы между различными теориями размыты, так как они не от-рицают друг друга, но развивают и дополняют. Так, КТП, занимающаяся свойствамиэлементарных частиц, родилась при соединении КМ и СТО, а ОТО (она же теориягравитации) --- при распространении СТО и классической механики на область боль-ших расстояний. Точка показывает электрон в атоме, свойства которого, как видно,попадают в сферу действия квантовой механики.

 Расчет радиуса орбиты и импульса электрона противоречит волновымидеям де Бройля, из которых мы и выводили эти характеристики. Нако-нец, совершенно непонятно, что же колеблется в пространстве при дви-жении электрона?

Контрольные вопросы

    • Что такое спектральные серии?

    • Сформулируйте постулаты Бора.

    • Какие значения могут принимать радиусы электронных орбит в атоме водородав теории Бора?

4. Какие значения может принимать скорость электрона, находящегося в поле ядрас зарядом +Zе? На основании полученного результата покажите, чтов природене могут существовать ядра с Z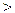 137.

 29.4. О границах применимости квантовой механики

125

    •  Какие значения может принимать энергия электрона в атоме водорода в теорииБора?

    • Как теория Бора объясняет спектральные серии?

    • В чем сущность гипотезы де Бройля?

    • Какова длина волны де Бройля у электрона с кинетической энергией, равной егоэнергии покоя?

    • Сформулируйте соотношения неопределенностей Гейзенберга.

    • Вообразите мир, в котором постоянная Планка имеет значение h =2000 Дж с.Живя в этом мире, Вы назначаете свидание, которое может состояться, если Вы иВаш партнер окажетесь в одном месте --- скажем, на расстоянии порядка x  1мдруг от друга. Будет ли у вас возможность спокойно пообщаться на свидании?

 Глава 30

Уравнение Шредингера

Вот мы и подошли к настоящей квантовой механике. Все, что было досих пор это интуитивные полуклассические представления, позво-

лившие инкорпорировать в классическую физику идеи физики кванто-вой. Но этот уровень знаний недостаточен для расчетов, количествен-ных предсказаний многих явлений. Требуется стройная система, те-ория движения (или распространения) микрочастиц с дуальными (волна-корпускула) свойствами.

    •  Волна вероятности

 Предыдущая глава закончилась констатацией, что мы пока не устано-вили, что именно колеблется при движении электрона. В истории фи-зики такое уже случалось. Когда-то при выводе уравнений электроди-намики Максвелл тоже не знал, что представляют собой описываемыеими колебания и волны, но уравнения оказались верны. Поэтому отло-жим пока вопрос о физической природе волн де Бройля и просто введемнекую ``электронную"" волну, т.е. функцию. О ней мы знаем покатолько одно: волновая функция должна описывать результаты опытов,доказывающих волновые свойства электронов (дифракцию и т.п.).

Представим мысленно эксперимент В. А. Фабриканта, в котором элек-троны поочередно направлялись на кристалл, играющий роль дифракци-онной решетки. За кристаллом помещена фотопластинка, на которой вконце концов возникают типичные дифракционные кольца. Из классиче-ской физики известно, какие математические средства описывают такуюкартину: обычное сложение интерферирующих волн, интенсивности ко-торых пропорциональны | 2 .

Правда, в отличие от обычной волны электрон не делится на части:

126

30.1. Волна вероятности

127

при прохождении электронов через кристалл каждый из них попадаетв какую-то одну точку на фотопластинке, вызывая почернение именноздесь и нигде больше. В этом проявляются свойства электрона как ча-стицы. Несмотря на одинаковые начальные условия электроны, как по-казал опыт, попадают в разные точки. О данном конкретном электронезаранее неизвестно, в какую именно точку на пластинке он попадет. Вэтом проявляются его волновые свойства. Дифракционная картина воз-никает, когда через кристалл пройдет достаточно много таких электро-нов. Интенсивность почернения пластинки в данной точке пропорцио-нальна числу попавших туда частиц, то есть вероятности попадания.

В классической же физике почернение пластинки определяется интен-сивностью волны, то есть квадратом модуля волновой функции. Выхо-дит, что | 2 пропорционален вероятности обнаружить электрон вточке  в момент времени t. Волна де Бройля --- это волна вероятно-сти! Отдельный акт взаимодействия электрона с кристаллом остаетсяотдельным актом (электрон-частица), но результат его можно предска-зать только вероятностно, статистически (электрон-волна). В этом ---смысл корпускулярно-волнового дуализма. Квантовая механика созданав 1925-27 гг. В. Гейзенбергом и Э. Шредингером; вероятностная ин-терпретация волновой функции дана чуть позже в работах М. Борна ишколы Н. Бора.

Итак, вероятность найти электрон в точке  должна быть пропорци-ональна | 2. Но вероятность обнаружить электрон точно в данномместе исчезающе мала; имеет смысл говорить лишь о его попадании вмалый объем dV, окружающий эту точку. Ясно, что вероятность dWобнаружить там электрон пропорциональна величине объема. Поэтомудля вероятности имеем

Иными словами, | 2--- плотность вероятности найти частицу вточке с координатой . Вероятность W(v)найти частицу в каком-токонечном объеме v вычисляется с помощью сложения вероятностей, т.е.интегрированием

Интегрирование в ведется по объему v (в случае одномерного дви-жения --- по отрезку). Полная вероятность найти частицу хоть где-нибудь в пространстве должна быть равна единице. Отсюда --- так на-

 dW= | 2dV.

                                                                                                         

128

Глава 30. Уравнение Шредингера

зываемое условие нормировки волновой функции: такой же интеграл повсему пространству равен единице, т.е.

Замечание: выполнение этого условия возможно для тех задач, в кото-рых классическая частица движется в ограниченной области простран-ства (финитное движение). Для других движений условие нормировкиусложняется.

Наблюдаемые физические величины должны описываться действитель-ными числами и функциями. Соответственно, мы представляли класси-ческие волны (звуковые, электромагнитные) в виде = A0cos(t- r   

 e-i = соs --- i sin,

где i=--- мнимая единица. Тогда ту же волну можно было быпредставить в виде действительной части выражения:

Волновая функция является главным объектом изучения в квантовой ме-ханике. Говоря о каком-то состоянии в классической физике, мы подра-зумевали, что в момент времени t= 0 частица имела некие положение и

30.2. Общее уравнение Шредингера

129

скорость (импульс), а дальнейшая ее судьба предопределена уравнениямидвижения Ньютона.

Состояние в квантовой механике имеет иной смысл: в момент времениt = 0 задана волновая функция, изменение которой регулируется пока неизвестным нам уравнением (Шредингера). В этом смысле теперь пони-мается причинность: в классике --- точные предсказания положений искоростей, в квантовой механике --- предсказания состояний (волновыхфункций). Уравнения новой физики (в данном случае --- уравнение Шре-дингера) никогда не выводятся логически из прежних принципов (иначеэто будет не новая теория, а следствие старой). Но квантовомеханическоеуравнение должно иметь некие классические корни, поскольку классиче-ская механика хороша в области своей применимости. Далее мы приве-дем не вывод, но наводящие соображения.

Свободной частице соответствует волна де Бройля, которую мы запи-сываем в виде классической плоской волны:

=.

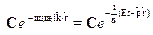 где модуль волнового вектора к связан с длиной волны соотношениемk =2/, а С --- амплитуда. Мы использовали уже известную связьэнергии и импульса частицы с частотой и длиной волны де Бройля. Ис-комое уравнение для волновой функции не должно содержать Е и р, таккак это --- характеристики конкретного состояния частицы. Попробуемнайти операции над волновой функцией свободной частицы, позволяю-щие исключить параметры Е и . Имеем для производной по времени

                                                                                                         

и по пространственной координате х

 .

Такие же уравнения возникнут при дифференцировании по у и z. Повто-ряя дифференцирование по координатам, получаем:

                                                                                                 

Складывая с аналогичными уравнениями для вторых производных

по у и 2, приходим к соотношению:

                                                

130

Глава 30. Уравнение Шредингера

где знаком  обозначен оператор Лапласа:

                                                      

В этом месте возникает различие между релятивистским и нереля-тивистским случаями. Квантовая механика --- нерелятивистская те-ория., в которой Е = 2/2m. Это классическое соотношение позволяетсвязать дифференцирование по времени в с дифференцированиемпо пространственным координатам в и тем самым исключить изуравнения зависимость от энергии и импульса частицы:

                                             

Это уравнение вполне бы нас устроило, но написано оно пока толькодля свободной частицы. Легко понять, как должно выглядеть уравнениедля системы с постоянным значением U0 потенциальной энергии. Полнаяэнергия равна сумме

                                                         

так что получаем

            

                                                                  

В случае частицы, находящейся в произвольном потенциальном полевблизи точки  потенциальную энергию можно считать постоянной ве-личиной U(), так что искомое обобщение почти с очевидностью следуетиз уравнения :

            

 Это и есть основное уравнение квантовой механики --- знаменитоеуравнение Шредингера. Подчеркнем еще раз, что вывести его строгоневозможно, но можно угадать, исходя из наводящих соображений. Соот-ветствие уравнения и его следствий физической реальности проверяетсяэкспериментально. Подчеркнем некоторые свойства :

Уравнение Шредингера по сути есть аналог классического соотноше-ния между полной энергией Е частицы и ее кинетической энергией2/2т. Для свободной частицы они совпадают. При наличии потен-циального поля это соотношение принимает вид Е = 2/2т + U().

30.3. Операторы, симметрия и законы сохранения

131

Мы уже знаем, что полной энергии соответствует производная по t,компонентам импульса --- производные по x, у, z, а кинетическойэнергии --- вторые производные по пространственным координатам,поскольку импульс входит в нее во второй степени. Классическойпотенциальной энергии, как мы видим, в квантовой механике соот-ветствует обычное произведение U() на волновую функцию.

Заметим, что уравнение Шредингера линейно по искомой волновой функ-ции. Отсюда сразу же вытекает, что

    • если ?r?

                                                                  

(t,)--- также егорешение при любой константе А. Следовательно, подбором постоян-ной А можно добиться выполнения условия нормировки ;

    • если ?r?

                                                                  

2 (t,)--- решения уравнения Шредингера, то линей-ная комбинация A1?r?

                                                                  

2 (t,) --- также его решение (принципсуперпозиции, т.е. основа явления интерференции).

    • Операторы, симметрия и законы сохранения

 Итак, состояние электрона описывается теперь волновой функцией ?r?

                                                                  

(t,). Из уравнения Шредингера видно, чтооно воспроизводит связь Е = Т + U полной энергии Е с кинетической Ти потенциальной U, но классические величины заменены на операторы,действующие на волновую функцию Ф. Будем обозначать оператор темже символом, что и классическую величину, снабжая его для отличияшляпкой. Тогда уравнение Шредингера можно записать в опера-торной форме, в которой отчетливо видна его связь с энергетическимисоотношениями классической физики:

 E??

                                                                  

+U?

132

Глава 30. Уравнение Шредингера

Здесь --- оператор градиента с компонентами:

                                                 

квадрат которого дает оператор Лапласа . Оператор координаты сводится к простому умножению ?rr  r p r р?

                                                                  

/?  p?

                                                                  

/?  p?

                                                                  

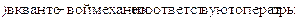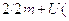/? р  r                                                       

В этих обозначениях уравнение Шредингера имеет вид:

                                                                                                       

Оператор полной энергии  называется гамильтонианом (аналог функ-ции Гамильтона в теоретической механике).

Очень важно! В классической механике законы сохранениясвязаны с симметрией системы: энергия --- с трансляцией (сдви-гом) времени t>t+t, импульс --- с трансляцией пространства>+ г 

                                                                 

    

                                                                  

).

 Трансляцию какой-то обобщенной координаты  производит оператордифференцирования по этой координате. Например, для бесконечно ма-лой трансляции q>q+q имеем по определению производной

                                          

Поэтому не случайно в квантовой механике полной энергии соответствует??

                                                                  

t, а импульсу --- градиент . Аналогично: оператор проекции мо-мента количества движения на какую-то ось z пропорционален оператору

30.4. Стационарное уравнение Шредингера

133

 дифференцирования ??

                                                                  

рпо углу поворота вокруг этой оси:

                                                        

    • Стационарное уравнение Шредингера

 В теории операторов важную роль играют так называемые собствен-ные состоянияоператоров. Это такие состояния, которые при действииданного оператора меняются тривиальным образом: умножаются на не-которое число. Это число называется собственным значениемданногооператора, соответствующим данному собственному состоянию. Чтобынайти собственные состояния и собственные значения какого-то опера-тора Анадо решить уравнение

А?  r?

                                                                  

п(t,) ,

 где индекс потличает одно решение от другого. Набор величин Ап,тоесть набор собственных значений оператора А, определяет его свойства.

Пример: операция поворота вокруг некоторой оси 2. Роль состоя-ний играют здесь обычные радиус-векторы. Очевидно, что при поворотевсе векторы меняются, кроме параллельных оси. Это и есть собствен-ные векторы оператора поворота вокруг оси 2, причем соответствующеесобственное значение равно единице. Аналогичны выводы для поворотавокруг осей ж и у. Произвольный поворот можно получить комбина-цией этих трех поворотов. Соответственно, любой радиус-вектор можнопредставить как линейную комбинацию трех собственных векторов г,] ,к.Ситуация с другими операторами по сути ничем не отличается от опи-санной: зная набор собственных состояний любое другое состо-

яние ?r

Связь математики с физикой реализуется в следующем правиле:

Правило 2 Измерение некой физической величины А всегда дает лишьодно из собственных значений Ап соответствующего ей оператора А.Вероятность получить при измерении именно значение Ап определя-ется состоянием системы (а именно, квадратом модуля Сп 2 соот-ветствующего коэффициента в разложении ).

 134

Глава 30. Уравнение Шредингера

Следствие: в собственном состоянии ?r?

                                                                  

е оператора полнойэнергии. Уравнение, согласно сказанному, имеет вид:

                                               

откуда следует решение

                                                                                                           

Мы получили общий вид состояния, в котором энергия имеет опреде-ленное значение. Такие состояния называются стационарными. Есте-ственно, пока невозможно сказать, чему равна энергия стационарногосостояния, поскольку мы еще не указали рассматриваемую физическуюсистему. В уравнении стоит некая функция ?

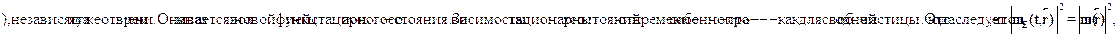
т.е. в стационарном состоянии плотность вероятности не зависит от вре-мени. В этом смысле и следует понимать название ``стационарное"". Под-ставляя решение в общее уравнение Шредингера , получимт.н. стационарное уравнение Шредингера, т.е. уравнение для ? r

Подчеркнем: это --- уравнение для состояний с определенной энергиейЕ. В операторных обозначениях оно имеет вид  = E , то естьпредставляет собой уравнение для собственных состояний гамильтони-ана. Задавая тот или иной вид потенциальной энергии, мы конкретизи-руем систему и получаем стационарное уравнение Шредингера, решениякоторого и описывают квантовые свойства системы.

Не следует думать, что система может быть только в стационарномсостоянии. Возьмем характерный пример: пусть и --- два не-ких стационарных состояния какой-то системы с разными энергиями E1

30.5. Уравнение Шредингера для простейших систем

135

и Е2. Предположим, что в начальный момент времени волновая функциясистемы является симметричной суперпозицией этих состояний:

Вопрос: что будет с системой в произвольный момент t

Зная, что справедлив принцип суперпозиции и что зависимость соб-ственных состояний от времени определяется соотношениями типа ,можно сразу же написать волновую функцию:

Плотность вероятности такого состояния зависит от времени! Введемобозначения для средней энергии Е = (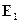 + Е2)/2 и частоты перехода = ( 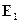--- Е2)/h. Тогда ., и легко получаем

вместо :

Видно, что в момент t = 0 система находится в симметричном со-стоянии, к моменту времени t = 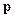/ она перейдет в антисимметричноесостояние, а в момент t = 2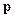/ --- снова вернется в симметричное со-стояние. Следовательно, система осциллирует между симметричным иантисимметричным состояниями с круговой частотой . Здесь усматри-вается аналогия с классической физикой: в рассмотренной ранее системесвязанных осцилляторов (см. Ч. 4, раздел 24.4.3) возникают похожиесобственные колебания (нормальные моды) и биения.

    • Уравнение Шредингера для простейших систем

Свободная частица, движущаяся вдоль оси х

 Потенциальная энергия равна нулю (U(х) = 0), и производные по у и zв операторе Лапласа исчезают. Уравнение принимает вид:

                                                 

         

  

 

 Введем волновой вектор k: Е = h2k2/2m, и перепишем уравнение в виде

 136

Глава 30. Уравнение Шредингера

Существует, как известно, два линейно независимых решения ,так что общее решение есть суперпозиция волн: стоячих

(первый член --- волна направо, второй --- налево; постоянные АиВпроизвольны). Аналогия: такие же решения описывают колебания сво-бодной струны. Поскольку возможны волны с произвольной частотой,то струна не звучит (т.е. энергия частицы не квантуется). Для ча-стицы, движущейся в произвольном направлении вдоль волнового век-тора , справедливы те же решения при замене kx>.

При решении большинства задач квантовой механики следует обра-тить внимание, что волновая функция должна быть непрерывной --- ве-роятность пребывания частицы не может меняться скачком от точки кточке. Если потенциал конечен, то из уравнения Шредингера следует,что первая производная также непрерывна.

Частица в бесконечно глубокой потенциальной яме

 Потенциал в этой задаче имеет вид:

Такая система соответствует частице, движущейся вдоль прямой линиии отскакивающей от абсолютно отражающих препятствий в точках х = 0и х = l. В область бесконечного потенциала частица проникнуть не мо-жет, следовательно ??

                                                                  

(х) = Аsin(kх) + Вcos(кх). Используем сначалапервое граничное условие:

 Asin(kx)+Bcos(kx)

 или бегущих

Аеiкх + Вei-кх

если 0  х  I,если х 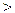 I или х  0.

 ??

                                                                  

(х) = Аsin(кх). Если продолжить нашу аналогию, то можно сказать,что на струне, закрепленной в одной точке, бегущих волн не бывает:отражение от неподвижной точки обязательно порождает стоячую волну.Однако на длину волны никаких ограничений не накладывается: такаяструна также не звучит.

Теперь наложим второе из граничных условий:

 ??

                                                                  

(х) = 0, чтоозначает отсутствие частицы в яме (вероятность найти ее всюду равнанулю). Поэтому нас интересует второе решение, когда sin(kl) = 0. Этовозможно лишь при некоторых значениях волнового вектора: kп = 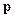n/1(п = 1, 2, 3,...). Так как энергия частицы связана с волновым вектором,то

             

Мы получили квантование энергии, то есть наша ``струна"", закрепленнаяс обеих сторон, зазвучала, так как появились выделенные частоты.

Подставляя найденные разрешенные значения волнового вектора в вы-ражение для волновой функции, получаем ее в виде:

                         

Смысл квантового числа п: оно на единицу больше числа нулей вол-новой функции. Значение постоянной А = у/2/7 определено из условиянормировки (см. задачи в последнем разделе этой главы).

Откуда же берется дискретность уровней энергии, характерная и дляатома? Сравним со свободной частицей: уравнения те же, но с инымиграничными условиями! Здесь возможны две постановки задачи. В пер-вом случае исследуется состояние, которому в классике соответствовалобы инфинитное движение (задача рассеяния). Обычно в таких случаяхрешения возможны при любых значениях энергии Е (как говорят, спектрнепрерывен). Во втором случае исследуется состояние, которому в клас-сике соответствует финитное движение в ограниченной области про-странства (задача на связанные состояния). Требование конечности вол-новой функции во всем пространстве ведет к квантованию энергии.

138

Глава 30. Уравнение Шредингера

Подчеркнем: в этом случае стационарное уравнение имеет физическиприемлемые решения не всегда, а лишь при некоторых значениях Е. Какследствие возникает дискретный спектр энергии системы.

Задача 30.21. Определить разность соседних уровней энергии Е длячастицы в бесконечной потенциальной яме при больших значениях п. По-лученный результат использовать для оценки разности соседних уровнеймолекул азота при комнатной температуре Т = 300 К в сосуде. Принятьмассу молекулы т = 2.3 10-26 кг, а линейный размер сосуда l = 0.1 м.Сравнить результат с кинетической энергией поступательного движениямолекул азота.

Решение. Используя выражение для уровней энергии частицыв потенциальной яме, находим разность энергий соседних уровней

                           

при больших значениях п. Кинетическая энергия поступательного дви-жения молекул азота равна Е = 3Т/2 ? 6, 21 10-21 Дж. ПриравниваяЕ и выражение для энергии уровней частицы в яме, находим, что такаяэнергия соответствует квантовым числам порядка

                                              

Уже само по себе это число говорит, что мы находимся в области крайневысоких возбуждений, то есть в области справедливости классическихзаконов. Разность соседних уровней получаем, подставляя в формулудля Е найденное выражение для квантового числа п:

                                         

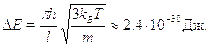
 В электронвольтах те же характеристики имеют значения Е 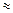 0.039 эВ,Е 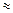 1.5 10-11 эВ. Относительная разность уровней ничтожно мала:Е/Е 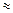4 10---10, и потому в классической физике квантовой дискретно-стью пренебрегают. ¦

Частица в трехмерной потенциальной яме

 Это --- обобщение предыдущей задачи. Частица может двигаться в ку-бическом объеме с длиной ребра l. Нетрудно убедиться, что общее реше-ние для волновой функции представимо в виде произведения одномерных

30.5. Уравнение Шредингера для простейших систем

139

волновых функций, полученных в предыдущей задаче:

        

Такая волновая функция соответствует очевидному факту, что движе-ния вдоль трех осей не зависят друг от друга и каждое описываетсяпрежними одномерными волновыми функциями. Энергия, как легко до-гадаться, будет равна сумме энергий движения по осям x, у, z:

Состояние системы теперь определяется тремя квантовыми числами , и , принимающими, как и прежде, целые значения. Здесь мы впер-вые сталкиваемся с важным понятием вырождения энергетических уров-ней, т.е. с ситуацией, когда разные состояния системы имеют ту жеэнергию. В самом деле, минимальная энергия системы достигается приминимальных значениях всех квантовых чисел, т.е. при  =  =  = 1.Эта энергия равна

                                                         

и ей соответствует одна волновая функция 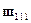 . Говорят, что основ-ное состояние не вырождено (невырожденность состояния с минимальнойэнергией --- общее правило). Первое возбужденное состояние получается,когда одно из квантовых чисел равно 2, а остальные по-прежнему равныединице; энергия его

                                                         

Но такую энергию имеют теперь три состояния с волновыми функциями(квантовое число, равное 2, можно выбрать тремя спо-собами). Говорят, что кратность вырождения первого возбужденногоуровня равна 3. Естественно, в другой системе может быть совершенноиная кратность вырождения (или отсутствие такового). Последующиесостояния частицы в потенциальной яме с бесконечными стенками такжевырождены. Ясно, что вырождение уровней связано с симметрией си-стемы, с равноправием всех осей, если бы размеры ямы были разными(l1, l2, l3) по всем трем направлениям, то для энергии мы бы получиливместо

           

                                            

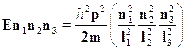
140

Глава 30. Уравнение Шредингера

и вырождение могло бы иметь место лишь при определенных соотноше-ниях между длиной, шириной и высотой потенциального ящика.

Одномерный осциллятор

 В классической физике система представляет собой тело, прикрепленноек пружине и колеблющееся с круговой частотой . Потенциальная энер-гия такой системы описывается выражением U(х) = m2x2/2, так чтоуравнение Шредингера записывается в виде:

                                      

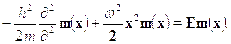
Отсюда можно найти решение для волновой функции основного состоя-ния:

                                            

 Подставляя ее в уравнение Шредингера, легко убедиться, что энергияосновного состояния равна Ео =  h

                                                                 

/2,полученные ранее из соотношения неопределенностей.

Трехмерный осциллятор

 Эта задача является обобщением предыдущей. Как и для трехмернойпотенциальной ямы с бесконечно высокими стенками, волновая функцияпредставляется в виде произведения волновых функций одномерных ос-цилляторов, колеблющихся независимо вдоль осей х,у,z. Так, волноваяфункция основного состояния имеет вид:

                                             

а уровни энергии трехмерного осциллятора описываются формулой

                                      

          

30.6. Принцип соответствия Бора

141

В отличие от одномерного осциллятора состояние определяется значе-нием трех квантовых чисел Легко понять, что все возбужден-

ные состояния должны быть вырожденными.

    • Принцип соответствия Бора

 Н. Бор на заре квантовой механики поставил вопрос о ее соотношениис классической. Обычные в нашем мире значения энергии велики посравнению с характерной энергией основного состояния и расщеплениемуровней: с высокой лестницы не различаем ступенек. Более научно: прибольших квантовых числах(высоколежащих уровнях) должны воспро-изводиться классические результаты. Покажем это на примере атомаводорода.

В главе 1 в разделе об атоме Бора было получено классическое выра-жение для скорости электрона на орбите радиусом R:

                                                      

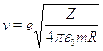
Отсюда легко получить классическую частоту вращения электрона:

                                            

Кроме того, было найдено классическое выражение для энергии элек-трона на орбите:

                                                         

позволяющее выразить радиус орбиты через энергию электрона:

                                                         

Подставляя это выражение в формулу для классической частоты враще-ния цс/, получаем

                    

Именно на этой частоте ожидается излучение электрона в классическойтеории.

142

Глава 30. Уравнение Шредингера

Кроме того, в том же разделе было выведено выражение для энергииуровня с номером п:

                                                      

При п 1 получаем отсюда квантовую частоту перехода 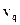 между со-седними уровнями:

                       

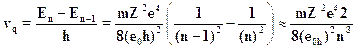
Выражая квантовое число п через энергию уровня, находим

                                                     

Подставляя это выражение в формулу для квантовой частоты переходамежду соседними высоко лежащими уровнями, приходим к окончатель-ному результату

                    

На этой частоте должен излучать сильно возбужденный атом Бора. Срав-нивая классическую частоту с квантовой , убеждаемся, чтопри той же энергии электрона они совпадают. Это свойственно не тольководородоподобному атому. Аналогичный результат получается для бес-конечной потенциальной ямы, этот же вывод можно сделать и для прочихсистем. Следовательно, соблюдается принцип Бора, и классическая ме-ханика действительно является предельным случаем квантовой.

Задача 30.22. Используя формулы и данные задачи 30.21., продемон-стрировать справедливость принципа соответствия Бора для молекулазота в сосуде.

Решение. При переходе молекул между уровнями с разностью энергийЕ излучается квант света с энергией hv = Е, откуда находим

                                                        

Кроме того, классическая скорость молекул азота равна v=и они пролетают сосуд от стенки до стенки и обратно за время  = 2l/v

30.7. Отражение и туннелирование частиц

143

(период классического движения). Обратная величина есть классическаячастота

                                                  

Именно на этой частоте классическая физика предсказывает электромаг-нитное излучение. Принцип соответствия Бора заключается в том, чтосовпадают обе частоты, квантовая (при переходах между высоковозбу-жденными состояниями) и классическая. То же самое справедливо, какмы видели, для атома Бора. Если подставить численные значения, тодля частоты излучения в данной задаче получится величина v ? 3.7кГц, что соответствует длине волны  = с/v ? 80 км --- сверхдлинныерадиоволны. ¦

    • Отражение и туннелирование частиц

 До сих пор мы имели дело с задачами на связанные состояния. Рассмо-трим теперь примеры инфинитного движения частиц, когда они могутуходить на бесконечно большие расстояния. В простейшем случае дви-жения вдоль одной из координатных осей задача рассеяния частиц сво-дится к задаче взаимодействия частицы с неким потенциальным барье-ром. Мы рассмотрим несколько типов барьеров простой прямоугольнойформы, чтобы усвоить характерные особенности этого типа квантовыхявлений.

Низкий бесконечный барьер

 Потенциальная энергия имеет вид:

U(x)=

Слово "низкий"" означает, что высота барьера U меньше энергии частицыЕ (рис. 30.1). Решим уравнение Шредингера отдельно для каждой изобластей. В области 1 потенциал равен нулю и мы имеем то же общеерешение для свободной частицы:

                                      

144

Глава 30. Уравнение Шредингера

Рис. 30.1: Низкий потенциальный барьер, пунктиром показана энергия налетающейслева частицы, цифрами --- номера областей с различной потенциальной энергией

 где А и В --- амплитуды падающей и отраженной волны, соответственно.В области 2 уравнение Шредингера имеет вид:

                                           

В этой области меняется кинетическая энергия (и импульс) частицы, имы должны ввести другой волновой вектор (обозначим его 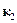 в отличиеот прежнего ):

                                                       

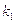Тогда очевидно, что решение уравнения Шредингера в области 2 будетиметь тот же вид, что и для области 1 с заменой на . Однако изфизических соображений ясно, что в области 2 не может быть волны,распространяющейся справа налево (в бесконечно удаленной точке ей неот чего отражаться). Поэтому волновая функция в этой области соот-ветствует прямой волне:

                                                       

По сути дела, здесь мы снова использовали некое граничное условие,хотя и иное, нежели для задачи о связанном состоянии. Нам осталосьопределить только амплитуды А, В, С.

Для этого мы должны вспомнить, что  и--- значения однойволновой функции в разных пространственных областях. Эта волноваяфункция должна быть непрерывна вместе со своей первой производнойпо переменной х. Непрерывность функции в точке х = 0 означает, чтодолжно выполняться условие

 ??

                                                                  

2, откуда А + В = С.

 Непрерывность первой производной волновой функции означает выпол-нение равенства

  =  (0) , откуда k1(А --- В) = k2С .

 30.7. Отражение и туннелирование частиц

145

Решение двух полученных уравнений дает

                                           

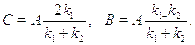
Амплитуда падающей волны остается не определенной: ясно, что оназависит от интенсивности потока частиц. Важны не сами амплитуды, аотношение R квадратов их модулей, т.е. интенсивностей отраженной ипадающей волн:

Величина R называется коэффициентом отражения частицы от низкогобарьера. По физическому смыслу это --- вероятность отражения частицы

называемая коэффициентом прохождения, определяет вероятность про-никновения частицы в правую область. Удивительно, что частица имеетшанс отразиться от низкого барьера и повернуть назад. В классическойфизике частица всегда (R = 0) проникает за барьер, если ей хватает наэто энергии. Например, с точки зрения классической физики электрон сэнергией 10 эВ, влетевший в конденсатор с тормозящим полем 5 В без-условно преодолеет торможение и продолжит свой путь с уменьшеннойэнергией 5 эВ. В квантовой же теории не равна нулю вероятность того,что электрон отразится от поля конденсатора и повернет назад. Коэф-фициент отражения можно измерить, направляя поток частиц на барьери измеряя долю отраженных от него частиц.

Высокий бесконечный барьер

 Потенциальная энергия имеет тот же вид, но энергия частицы меньшевысоты барьера: Е  U(рис. 30.2). Решение в области 1 остается преж-ним: суперпозиция прямой и отраженной волн. В области же 2 из-заобратного соотношения между энергией частицы и высотой барьера вол-новой вектор становится мнимым:

                                         

                                           

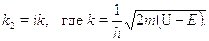
от барьера. Соответственно, величина D = 1 --- R= 4/( 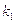+ 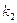)2,

При подстановке мнимого волнового вектора 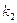 = iк в выражение для коэффициента отражения R получаем, что B = 1. Как и в классике,частица с энергией, меньшей высоты бесконечного барьера, наверняка

146

Глава 30. Уравнение Шредингера

Рис.30.2: Высокий потенциальный барьер

Рис.30.3: Конечный потенциальный барьер

отразится от него. Правда, в классической физике частица вовсе не мо-жет проникнуть под барьер. Наше же решение уравнения Шредингерадля области 2 в случае высокого барьера становится равным

                                                        

Это уже не совсем волна, а экспоненциально затухающая функция. Каки в случае низкого барьера, отброшено нефизическое решение --- экспо-ненциально растущая функция вида еzх. Под глубиной проникновениячастицы под барьер d принято понимать расстояние, на котором интен-сивность потока (вероятность) ослабевает в е раз. Из выражения для следует, что d = 1/(2к).

Конечный потенциальный барьер

 Потенциальная энергия имеет вид:

Ясно, что происходит при Е 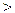 U : с некой вероятностью частица может

 отразиться от барьера. Наиболее интересен случай Е  U (рис. 30.3).Мы видели, что интенсивность (квадрат модуля амплитуды) волны убы-вает под барьером и на расстоянии (I становится меньше в ехр( ---2dk) раз.Но в этой точке барьер кончается, так что волна выйдет на свободу суменьшенной амплитудой. Отношение интенсивностей выходящей и па-дающей волн называется коэффициентом прозрачности D (он же равен

30.7. Отражение и туннелирование частиц

147

вероятности прохождения через барьер). Из наших рассуждений следуетприближенное выражение для него:

Получая D, мы опустили некие множители перед экспонентой, что пофизическому смыслу означает пренебрежение процессами, когда частица,прежде чем выйти из-под барьера, испытает многократное отражениеот его стенок. При высоком и широком барьере (D 1) вклад такихпроцессов невелик и сделанное приближение оправдано.

Проникновение частицы сквозь конечный потенциальный барьер воз-можно в квантовой механике, но категорически запрещено классической.В самом деле, формально вектор hк играет роль импульса (мнимого),так что кинетическая энергия Т=-h2к2/2m становится отрицатель-ной. Дело спасают соотношения неопределенностей. Модуль (мнимой)скорости частицы имеет порядок v?hк/т, так что время туннелиро-вания t ? dт/hk. Неопределенность в ``кинетической"" энергии Т ?h/2t ? h2к/2dm. Из полученных результатов для коэффициента про-зрачности видно, что эффект туннелирования заметен, если kd 1. Нотогда

Получается, что неопределенность в кинетической энергии частицы подбарьером больше самого значения кинетической энергии. Поэтому нельзяутверждать, что под барьером кинетическая энергия отрицательна. Ско-рее, она ``размыта"" настолько, что частица может как бы перепрыгнутьне слишком большой барьер. В случае же высокого и широкого барьера``размытость"" кинетической энергии должна быть очень велика, что воз-можно лишь на очень короткое время, за которое частица не успеваетпроскочить за барьер. Поэтому в этом случае коэффициент прозрачно-сти становится экспоненциально малым. По-другому: туннелированиезаметно при ширине барьера порядка длины волны де Бройля.

Барьер произвольной формы можно представить в виде последователь-ности прямоугольных барьеров; теорема об умножении вероятностей ве-дет к появлению суммы (интеграла) в экспоненте, так что вместо имеем

D?exp(-2kd) =exp

                                                   

              

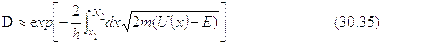
148

Глава 30. Уравнение Шредингера

Рис. 30.4: Частица в потенциальной яме, образованной непроницаемым препятствиеми конечным барьером

 Интеграл берется между точками поворота (U () = Е), в которыхклассическая частица должна изменить направление движения.

Задача 30.23. Электрон находится в одномерной потенциальной яме ши-риной а = Ю-10 м (рис. 30.4) и имеет энергию Е = 1.5 эВ. С одной сто-роны ямы потенциальная энергия V(х) бесконечна, а с другой сторонывыйти из ямы электрону мешает потенциальный барьер высотой U = 2эВ и шириной d = 3 10-10 м. Оценить время жизни  электрона в яме.

Решение. Скорость электрона в яме v= и за промежутоквремени t он подойдет к барьеру vt/2а раз. При каждом подходе веро-ятность туннелирования равна так что вероятность туннелированияза время t равна

                                                 

Вероятность  увеличивается с ростом промежутка времени t. Принекотором значении t =  вероятность туннелирования станет равнойединице и электрон вырвется из ямы. Отсюда получаем для временижизни электрона в яме оценку:

Теперь остается подставить численные данные. Для упрощения вычи-слений имеет смысл отдельно рассчитать коэффициент прозрачности ипред экспоненциальный множитель. Имеем:

                              

                      

30.7. Отражение и туннелирование частиц

149

Теперь осталось рассчитать коэффициент прозрачности:

          

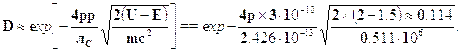
Получаем окончательно:

                                    

Даже по масштабам микромира это время мало: прежде чем электронпросочится сквозь барьер свет успеет пройти расстояние всего лишь в0.7 мкм. ¦

Прозрачность барьера сильно зависит от энергии частицы в яме и отширины и высоты барьера. Например, при увеличении ширины барьерав два раза новый коэффициент прозрачности будет равен, как легко до-гадаться, квадрату старого. Для электрона тогда получится значениеD = 0.0013 и его время жизни в яме увеличится до  = 21 фс. Это иобъясняет отсутствие туннелирования в обычном мире с его высокими иширокими потенциальными барьерами.

Задача 30.24. Решить предыдущую задачу, если вместо электрона в туже яму помещен протон.

Решение. Чтобы не решать аналогичную задачу с самого начала, можновоспользоваться результатами предыдущей. Протон массивнее электронав п = 1836 раз. В коэффициент прозрачности масса частицы входитпод квадратным корнем в показателе экспоненты. При изменении массыв п раз в показателе экспоненты появится множитель  и новый ко-эффициент прозрачности будет равен старому, возведенному в степень =  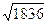?42.85. Используя данные предыдущей задачи, получаем

                                             

Предэкспоненциальный множитель также умножится на л/п и время жизнипротона в потенциальной яме будет равно

                               

150

Глава 30. Уравнение Шредингера

Получилась столь огромная величина, что протон будет жить в ямевечно: время существования Вселенной ``всего"" 15 млрд лет. ¦

Эти две задачи демонстрируют сильную зависимость проницаемостибарьера от массы частицы.

    • Оптическая аналогия прохождения частицы надбарьером

 В этом разделе мы покажем, что прохождение квантовой частицы черезнизкий потенциальный барьер аналогично отражению света на границедвух полубесконечных сред. Далее, прохождение частицы через потенци-альный барьер конечной ширины может быть описано как множественноеотражение классических волн, и в результате опять-таки мы придем кизвестным результатам оптики. Целью данного раздела является демон-страция тесной связи различных областей физики.

Ступенчатый потенциал

 Этот потенциал мы снова изобразим на рис. 30.5.

Рис. 30.5: Прохождение частицы над ступенчатым барьером эквивалентно нормальномупадению света из вакуума на полубесконечную среду с показателем преломленияп = 1/ 

 Установление аналогии между квантовой механикой и светом озна-чает, что мы хотим найти такие замены квантовомеханических харак-теристик движения частицы на характеристики света, чтобы формулыквантовой механики перешли в соответствующие формулы для распро-странения света. Процедура замены будет изображена в формулах двой-ными стрелками, причем слева будут стоять квантовомеханические ве-личины, а слева --- оптические. От этих формул следует отличать равен-

30.8. Оптическая аналогия прохождения частицы над барьером

151

ства, где по обе стороны стоят величины, относящиеся либо к частице,либо к световой волне.

Распространение квантовой частицы описывается в терминах ее вол-нового вектора, ,где Т --- кинетическаяэнергия частицы. Здесь и далее мы выписываем для частицы формулы,относящиеся к области барьера; соотношения для частицы вне барьераполучаются при U= 0. Скорость частицы дается соотношением:

Введем прежде всего показатель преломления п среды 2, соответствую-щей области барьера: его естественно определить, как отношение скоро-стей частицы в областях 1 и 2:

                      

                     

При U = 0 получаем n = 1 --- показатель преломления вакуума.

Волновой вектор световой волны связан с круговой частотой соотноше-нием k = т/с. Мы предположим также, что волновой вектор частицыперейдет при искомой замене в волновой вектор света, т.е.

                                        

Из соотношения =kc/n для среды без дисперсии следует группо-вая скорость света d/dk=c/n, в которую при искомой замене должнаперейти скорость частицы v. Тогда уравнение дает:

                                                            

 Разделив уравнение на , находим еще одну замену:

                                                         

Конечно, ``масса"", стоящая здесь в правой части, ничего общего не имеетс массой фотона, которая равна нулю. Можно назвать ее ``эффективноймассой фотона в среде"", и в вакууме, при n = 1, она равна h/. Этавеличина соответствует известной релятивистской связи масса-энергия,и она возникает при изучении влияния гравитационного поля на распро-странение световых лучей.

152

Глава 30. Уравнение Шредингера

Как бы то ни было, но суть в том, что указанные замены, как мыувидим, переводят формулы квантовой механики в формулы оптики.

Рассматривая прохождение частицы над низким потенциальным ба-рьером (см. ступенчатый потенциал на рис. 30.5), мы уже вывели коэф-фициент прохождения, который здесь обозначим D8:

Коэффициент отражения R8 = 1 --- D8 переписываем в виде:

                                         

Применяя вышеуказанные замены, сводящиеся в данном случае к за-мене k1/k2 ---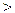 n, мы записываем соответствующие коэффициенты прохо-ждения и отражения для света, падающего перпендикулярно из вакуумана среду с показателем преломления п:

                                          

В оптике точно такие формулы называются формулами Френеля для от-носительной интенсивности отраженного и преломленного света при углепадения 90. Мы еще раз убедились, что физика (или природа) --- едина,и квантовая механика имеет глубокие корни не только в классическоймеханике, но и в волновой оптике.

Прямоугольный барьер конечной ширины

 Потенциальный барьер показан на рис. 30.6. Решение задачи можно вы-полнить стандартным образом, записывая суперпозицию плоских волндля каждой из трех областей 1, 2 и 3 и сшивая затем решения, чтобынайти амплитуды волн. Однако мы заменим такой рутинный способна классическое рассмотрение прохождения волн, что позволит выявитьфизический смысл получающегося результата.

Заметим прежде всего, что конечный барьер можно рассматриватькак наложение двух ступенчатых барьеров, расположенных в точках х =x0 и х = x0 + d. Это замечание дает возможность использовать ранееполученные формулы.

153

30.8. Оптическая аналогия прохождения частицы над барьером

Рис. 30.6: Прохождение частицы над конечным прямоугольным барьером.Процессэквивалентен многократным отражениям от барьера, показанного на рис.30.5.

 Пусть квантовая волна с амплитудой, равной единице, движется слеванаправо и проникает в область над барьером в точке . Вследствиечастичного отражения ее амплитуда уменьшается и становится равной  , где D8 --- коэффициент прозрачности ступенчатого барьера. Далееона распространяется до точки х =  + d, приобретая на пути сдвигфазы  по сравнению с фазой свободной частицы в этойже точке. Здесь она волна снова встречается со ступенчатым барьером,и в результате ее амплитуда вновь уменьшается на множитель . Врезультате волна выйдет за барьер с амплитудой

                                                                                                     

Но мы учли только часть волны, выходящей наружу. Пришедшая вточку х = x0 + d волна частично отражается от нее (дополнительныймножитель  в амплитуде), идет назад в точку x=x0, снова отража-ется там (множитель ), возвращается назад в точку х = x0 + d гдеи выходит наружу. Полный пройденный этой частью волны путь равен37, что дает сдвиг фазы .В результате эта часть волнывыйдет за барьер с амплитудой

.

Аналогичным образом происходят процессы с 2п отражениями внутрибарьера, и каждый из них приводит к волне с амплитудой

.

Амплитуда Аr результирующей волны получается суммированием вы-ражения по всем га от нуля до бесконечности:

                       

154

Глава 30. Уравнение Шредингера

Модуль амплитуды Аrпрошедшей над барьером волны даст нам ко-эффициент прохождения Dг:

    

Подставляя сюда квантовомеханическое выражение для R8, полу-чаем:

                                         

Стандартное решение уравнения Шредингера дает в точности такой жерезультат. Переходя к оптике, заменяем R8 на выражение и k2 ---на n/с. Получаем тогда коэффициент прозрачности образца конечнойтолщины d при нормальном падении света с частотой :

      

Это выражение также в точности воспроизводит результат волновойоптики.

Подобным образом можно рассмотреть отраженную от барьера волну,но результат нам уже известен: коэффициент отражения от конечногобарьера можно вычислить по формуле Rr= 1 --- Dr.

Изучая формулы и , мы обнаруживаем ``окна прозрач-ности"" при некоторых значениях частоты падающего света, когда Dr =1,R8 = 0, т.е. нет никакой отраженной волны. Это случается при т = 1,2,3,..., т.е. когда четное число полуволн (или це-лое число волн) света е среде укладывается в двойной ширине барьера:2d = т2. В обратном случае, когда двойная ширина барьера равнанечетному число полуволн (2d = (2т + 1)2/2), мы приходим к мини-мальному значению коэффициента прозрачности:

                  

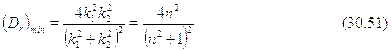
В случае Е  U0 мы имеем дело с туннелированием --- частица ``дви-жется"" внутри барьера с ``мнимым"" волновым вектором

                                            

(30.52)

30.8. Оптическая аналогия прохождения частицы над барьером

155

В этом случае тригонометрическая функция перейдет в гиперболическую, и из уравнения следует выражение длякоэффиц)иента прохождения:

                                               

Если, как это обычно бывает, аргумент,d то доминирует членс гиперболическим синусом, причем s. Пренебре-гая также пред экспоненциальными множителями, получаем уже знако-мое выражение :

                  

Прохождение света через многослойную структуру

 В этом разделе мы рассмотрим прохождение частицы над потенциаль-ным барьером, составленным из N прямоугольных конечных барьеровшириной d, причем межбарьерное расстояние всюду одинаково и равно b(рис. 30.7).

Рис. 30.7: Многослойная структура с периодом l=d+b, образованная N прямоуголь-ными потенциальными барьерами шириной d и межбарьерным расстоянием b.

 В принципе решение задачи о нахождении коэффициента прохождения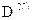через такой барьер может быть решена описанными выше спосо-бами. Сейчас нам важно только понять основной физический результат,так что нижеследующие формулы приводятся без вывода и только длясправки. Выражение для коэффициента прохождения имеет вид:

                       

 156

Глава 30. Уравнение Шредингера

Где  --- коэффициент прохождения через одиночный прямоугольныйбарьер, вычисленный выше (при N= 1 получаем из = Dг).

Величина k называется квазиволновым вектором (для отличия от вол-новых векторов частицы  и мы набираем ее прямым шрифтом).

В случае света мы используем для Dr результат . Связь квази-волнового вектора с частотой падающего света и показателем преломле-ния дается тогда выражением:

где

kl=

                        

Наконец, входящие в функции определены как

sin[h]x=

Ясно, что для частот, при которых абсолютно прозрачен прямоуголь-ный барьер (Dг = 1), будет прозрачен и наш составной барьер ( = 1в этом случае, как следует и из формулы ). В дополнение по-явятся и новые окна прозрачности. Здесь ситуация очень похожа наслучай с дифракционной решеткой (см. Ч. IV, раздел 30.5). Числен-ное решение показано на рис. 30.8, где для конкретности мы положилип = 1.52,b = 0.9(7. Левый рисунок представляет собой коэффициент про-хождения для одного, двух и четырех барьеров, правый --- для десятибарьеров. Последний случай, когда число барьеров велико (N1)представляет для нас особый интерес. Тенденции, обнаруживающиесядля N = 10, в пределе N> станут только отчетливее. А именно: сростом N некоторые минимумы становятся глубже и шире, и в пределезначение коэффициента прохождения в них стремится к нулю. Наоборот,амплитуда колебаний при других частотах становится меньше и

коэффициент прохождения стремится к единице. Физическое объяснениеэтого явления заключается в том, что выполнении определенных условийотраженные от концов прямоугольных барьеров волны взаимно компен-сируют, гасят друг друга.

Подчеркнем еще раз: для предельного случая периодической струк-туры (N> ) зависимость коэффициента прохождения от частоты

падающего света такова, что

30.8. Оптическая аналогия прохождения частицы над барьером

157

а

к

X

ф

о

X

о

о.

п.

-

X

ф

-8-

-8-

о

о

Рис. 30.8: Коэффициент прохождения в зависимости от частоты падающего света для малого (слева) и большого (справа) числа барьеров. Видна тенденция формированияпри N>  широких минимумов (т.н. запрещенных зон, непрозрачных для света иличастицы) и максимумов с D>1 (т.н. разрешенных, абсолютно прозрачных зон).

    •  имеются целые полосы частот, в которых 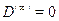 ; для таких ча-стот составной барьер непрозрачен, свет этих частот полностью от-ражается от структуры.

    • для других же частот, наоборот,= 1, т.е. для них барьер пол-

 ностью прозрачен, не происходит никакого отражения, свет свободно

распространяется в такой структуре (на этом явлении основано со-здание т.н. просветленных объективов).

Аналогичное явление происходит и для квантовомеханической частицы,распространяющейся в периодическом потенциальном поле. При некото-рых значениях энергии частицы бесконечная периодическая последова-тельность потенциальных барьеров становится для нее совершенно не-прозрачной, даже если энергия частицы превышает высоту барьера. Придругих энергиях, наоборот, периодическая потенциальная структура ста-новится для частицы абсолютно прозрачной. Так возникают запрещен-ные и разрешенные энергетические зоны в кристалле, и мы с ними в своевремя познакомимся поближе.

Контрольные вопросы

    • В чем заключается вероятностная интерпретация волновой функции?

 158

Глава 30. Уравнение Шредингера

    •  Что такое условие нормировки волновой функции и в чем его физический смысл?

    • Запишите общее уравнение Шредингера. Какому соотношению классической фи-зики оно соответствует?

    • Как действует на волновую функцию оператор импульса ?

    • Как действует на волновую функцию оператор координаты г и любая функцияэтого оператора f?

    • Что такое гамильтониан системы?

    • Запишите стационарное уравнение Шредингера.

    • При решении стационарного уравнения Шредингера для некоторой системы полу-чается ряд значений энергии: . .. Может ли экспериментатор получить

какое-то иное значение при измерении энергии этой системы?

    • Что такое вырождение энергетических уровней?

    • Дайте наглядное объяснение, почему квантуется энергия частицы, находящейся вбесконечно глубокой потенциальной яме.

    • Что такое нулевые колебания квантового осциллятора? Почему их существованиенеизбежно?

    • * Сформулируйте принцип соответствия Н. Бора.

    • В бесконечно глубокой потенциальной яме расстояние между высоколежащими

уровнями возрастает с ростом номера уровня п (см. (30.24)). В то же время, ка-залось бы, принцип соответствия Бора требует, чтобы уровни сгущались к клас-сическому значению. Покажите, что принцип соответствия справедлив и для

этой системы.

    • Пусть частица налетает на потенциальный барьер, причем ее энергия большевысоты барьера: Е  U. Можно ли по результату такого процесса обнаружитьразницу между предсказаниями классической и квантовой теорий?

    • Что такое эффект туннелирования? Почему он не наблюдается в нашей повсе-дневной жизни?

    • Металлическая шайба массой т = 10 г скользит по гладкой поверхности соскоростью  = 1м/с. На ее пути стоит небольшая горка с гладкими скло-нами. Высота горки Н = 5.5 см, ее ширина d = 10 см. Как известно из курсамеханики, начальная скорость шайбы позволяет ей подняться лишь на высоту = = 1/(2 X 9.8) = 5.1 10-2 м = 5.1 см. Квантовая же механика утвер-ждает, что в принципе шайба может оказаться по другую сторону горки. Оценитьвероятность такого события.

    • Квантовая механика дает только вероятностное описание движения частиц, гово-рить об их положении, скорости и т.п. смысла не имеет. Как Вы думаете, кактогда эта теория может широко использоваться при проектировании, например,устройств, использующих квантовые свойства систем?

 Глава 31

Теория атома

Раз уж мы получили в руки такое мощное оружие, как уравнение Шре-дингера, то естественно вернуться к атому, начав с простейшего ---- атома водорода. Надо же убедиться, что квантовая механика при-ведет к тем же результатам, что и полуклассическая теория атома поБору. К тому же есть надежда, что новая теория подарит нам неожи-данные открытия. Жаль только, что изучение способов решения урав-нения Шредингера не входит в рамки настоящего курса. Но не беда:мы постараемся обойтись без излишней математики, угадывая свойстварешений на основе интуиции, выработанной при изучении классическойфизики. Следует только помнить, что читателя никто обманывать несобирается: все ``угаданное" может быть получено из уравнения Шре-

дингера точными математическими расчетами.

 31.1 Коммутирующие операторы

В предыдущей главе мы установили, что классические динамические пе-ременные заменяются в квантовой механике на операторы, действующиена волновую функцию. Результатами измерения некой величины А все-гда будут собственные значения соответствующего оператора: Ап =Апп. Если система находится в каком-нибудь собственном состояниип оператора А, то измерение наверняка дает собственное значение Ап.Если же система находится в каком-то другом состоянии, то измерениеА с определенной вероятностью дает какое-то из собственных значений,причем эта вероятность зависит от волновой функции состояния и, ра-зумеется, от измеряемой величины А.

 Пусть система находится в состоянии с определенным значением ве-личины А. Это значит, что ее волновая функция является собственной

 159

160

Глава 31. Теория атома

функцией оператора А. Может ли другая величина В также иметь опре-деленное значение? Иначе, может ли состояние быть собственным сразуи для оператора А, и для В?

Правило 3 Два оператора А и В имеют общий набор собственных со-стояний тогда и только тогда, когда они коммутируют:

 АВ = В А .

Иначе: если результат последовательного действия двух операторов независит от порядка, то соответствующие величины могут одновременноиметь определенные значения. Рассмотрим пример:

                                        

                                             

то есть для любой функции

                                                   

или просто

                                                      

Поскольку эти операторы не коммутируют, то координата и проекцияимпульса на ту же ось не измеримы одновременно. Этот вывод и естьистинный источник соотношения неопределенностей Гейзенберга, физи-ческий смысл которых разобран выше.

Особое значение имеет свойство коммутации операторов с гамильто-нианом, т.е. с оператором полной энергии . Если какой-то оператор 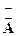коммутирует с , то существует общее собственное состояние, котороестационарно по определению. В стационарном же состоянии система пре-бывает неограниченно долго. Это означает одновременно и сохранениевеличины А. Таким образом, утверждение о сохранении некой величиныэквивалентно тому, что она может иметь определенное значение вместес энергией, т.е. соответствующий ей оператор коммутирует с гамильто-нианом.

31.2 Момент количества движения

В классической механике момент количества движения (его также на-зывают моментом импульса или угловым моментом) выражается в виде

31.2. Момент количества движения

161

векторного произведения радиус-вектора на импульс: =. То жесоотношение верно для операторов квантовой механики:

                                                 

или по компонентам

                                                                                                       

и аналогично для других компонент. В главе 2 обсуждалось, почемуоператор проекции момента количества движения на какую-то ось связанс производной по углу поворота вокруг этой оси (см. уравнение (2.14)). Всферических координатах поворот вокруг оси z эквивалентен сдвигу поазимутальному углу , и потому оператор имеет особенно простойвид:

Выражения для других компонент  и 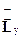 в сферических координатахдовольно сложны, и мы выпишем здесь лишь оператор квадрата моментаколичества движения:

                             

Выражение также достаточно сложно, и мы его практическииспользовать не будем. Но даже только глядя на него, уже можно сделатьважные выводы.

В оператор  входит не сам угол , а лишь производная по нему.Это означает, что  коммутирует с оператором .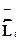

    • Так как ось z ничем не выделена, то оператор квадрата моментаимпульса коммутирует и с операторами проекции момента импульсана любую другую ось (в частности, с 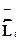. и .).  

 Из не выписанных здесь выражений для .и . следует, что опера-торы ...не коммутируют, между собой.

Вместо формального математического доказательства последнего утвер-ждения укажем источник этого свойства. Напомним, что .. явля-ются операторами поворота системы вокруг осей х,у,z, соответственно.

 162

Глава 31. Теория атома

х

х

Рис. 31.1: В верхнем ряду Г-образная фигура (а) сначала поворачивается на 90 вокругоси y(b) затем --- вокруг оси x (с). В нижнем ряду выбрана обратная последователь-ность тех же поворотов. Конечный результат (с) получился другим.

 Но результат двух таких поворотов зависит от их последовательности(рис. 31.1).

Из сказанного вытекает важное следствие: одновременно измеримылишь квадрат момента импульса и одна из его проекций (в качестветаковой обычно выбирают 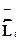). Это значит, что вектор  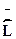в кван-товой механике не имеет определенного направления и его нельзясчитать классическим вектором с тремя определенными компонен-тами.

Квантовый момент количества движения можно условно представитьсебе как вектор фиксированной длины (определенное значение квадратамомента импульса), направленный под фиксированным углом к оси 2(определенное значение проекции), но прецессирующий вокруг этой оси(другие компоненты не определены). Это --- не более чем механическаяаналогия, но она верно отражает существенные свойства момента им-пульса в квантовой механике.

Найдем теперь собственные функции и значения оператора 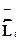 . Имеемуравнение:

                                                  

                                                        

откуда

31.2. Момент количества движения

163

При повороте на угол 2 система возвращается в первоначальное состо-яние. Чтобы волновая функция  не изменилась, необходимо выпол-нение условия =hm где m--- целое (не обязательно положительное)число. Константа А определяется условием нормировки: интеграл от| по углу , изменяющемуся от 0 до 2, должен быть равенединице, откуда А = 1/.

Таким образом, мы приходим к квантованию проекции момента им-пульса, которая может принимать лишь целые значения в единицах по-стоянной Планка (hm, где m= 0, 1, 2,...). Число m называют маг-нитным квантовым числом. Собственная волновая функция соот-ветствующая данному значению ш, имеет вид

                                                    

По сути дела, волновая функция описывает плоскую волну, бе-гущую по окружности. Роль координаты играет угол , роль волно-вого вектора --- магнитное квантовое число т. Но значения перемен-ной  ограничены пределами 0 и 2. Наша ``круговая"" волна как-бызаключена в потенциальную яму и совершает финитное движение.Отсюда --- квантование проекции момента импульса, в соответствиис установленными выше законами квантовой механики.

 Найдем теперь правила квантования квадрата момента импульса. Ре-шение соответствующего уравнения на собственные функции оператора

  достаточно сложно, и мы заменим его не очень строгими, но простымисоображениями. Пусть в какой-то системе максимальная величина маг-нитного квантового числа m равна целому неотрицательному числу l.Тогда минимальное значение m, очевидно, равно --- l, так что m пробе-гает 2l + 1 возможное значение:

 m=-l.-l+l ..-1.0.1  l-1.l.

 В классическом случае максимально возможная проекция момента им-

 пульса совпадает с модулем вектора . Но не следует ожидать, что

оператор  будет иметь собственные значения /г2/2. Мы уже знаем,что даже при максимальной величине проекции момент импульса не па-раллелен оси z (иначе были бы известны все три компоненты момента).

Стало быть, собственные значения оператора  должны быть больше

. Чему же они равны?

164

Глава 31. Теория атома

Если в пространстве нет выделенного направления, то любое значениет равновероятно, и среднее значение квадрата проекции момента на осьz равно

                                     

При выводе использовалась известная формула для суммы квадратов це-лых чисел. Заметим, что все три координатные оси равноправны, следо-вательно тот же результат справедлив для средних значений квадратовостальных операторов проекции момента импульса:

                                          

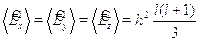
Но их сумма дает квадрат оператора момента импульса, среднее значе-ние которого равно, таким образом,

                                                                                                               

Именно этой формулой описываются собственные значения оператораквадрата момента импульса, так что условно можно считать, что длинавектора  в квантовой механике равна. Целое неотрицатель-ное квантовое число l называют азимутальным квантовым числом.

Для сравнения получим тем же способом классический ответ. Еслиl --- максимальное значение mдля классического вектора, то т пробе-гает непрерывный ряд значений от --- l до lс равной вероятностью dm/2l.Разница в том, что из-за непрерывности сумма заменяется на интеграли мы получаем:

                                  

и аналогичные выражения для двух других средних. Складывая их, при-ходим к обычному результату классической физики:

                                                         

При больших значениях l оба результата совпадают (опять --- принципсоответствия Бора).

31.2. Момент количества движения

165

m = +1m = 0m = -1

Рис. 31.2: Возможные положения вектора момента импульса при l=1. Длина вектораравна , а его проекция на выделенную ось может принимать только значения 0 и 1(в единицах h).

 Главный итог этого раздела --- знакомство с правилами квантованиямомента импульса: собственное значение квадрата момента импульсаопределяется величиной азимутального квантового числа /, а проекциямомента импульса --- величиной магнитного квантового числа т, кото-рое может принимать любое из значений 0, 1,... , /. Если все-такипытаться представить себе квантовый вектор момента количества дви-жения как обычный вектор, то можно сказать, что при данной длинеэтого вектора он составляет с выделенной осью лишь строго определен-ные углы (рис. 31.2). Подчеркнем еще раз, что эта картинка --- всеголишь попытка изобразить квантовыесвойства в классическихобразах.

Задача 31.25. Показать, что согласно квантовой механике направлениемомента импульса  не может совпадать с выделенным в пространственаправлением и что в пределе больших азимутальных чисел l1 вос-станавливаются классические свойства.

Решение. Поскольку модуль вектора момента импульса принимает зна-чения h, а его проекция на выделенное направление равна /hm,m=-l.-l+1  l,-1,l , то можно ввести угол  между направлениеммомента импульса и выделенной осью, так что соs  будет приниматьлишь определенные значения

                                                      

Отсюда следует, что минимальное значение угла  определяется макси-мальным значением его косинуса, достигаемым при т = l:

                                                      

Видно, что при любом конечном значении l угол не равен нулю. Напри-мер, для р---состояний l= 1и cos = 1 /, то есть  = 45, а для

166

Глава 31. Теория атома

f --- состояний с l = 3 имеем соs min = и min = 30. Видно, что

с ростом l минимальный угол между моментом импульса и осью умень-шается и в пределе l >? получаем min = 0. Это и есть классическоесвойство момента импульса: способность быть в точности параллельнымлюбому выделенному направлению. ¦

    • Атом водорода

 Стационарное уравнение Шредингера для водородоподобного атома (одинэлектрон около ядра с зарядом Zе) имеет вид:

                                       

Разумеется, мы не станем решать это уравнение, но просто внимательнона него посмотрим.

Заметим, что та часть уравнения , которая зависит от углов, вхо-дит только в составе оператора квадрата момента импульса . До-вольно ясен физический смысл этого члена. Представим себе, что в полецентральных сил по орбите радиусом г движется классическая частица симпульсом  . Ее момент количества движения равен ,где --- проекция импульса на направление, ортогональное радиус-вектору r. Обозначим кинетическую энергию ``ортогональ-ного"" движения. Ее можно выразить через квадрат момента количествадвижения:

                                                        

Этот член добавляется к потенциальной энергии кулоновского притяже-ния к ядру и его можно интерпретировать как потенциальную энергиюв поле центробежных сил. Действительно, если  --- потенциальнаяэнергия, то ее производная по r должна дать соответствующие силы:

                                      

Это уравнение удобно записать в сферических координатах:

                 

31.3. Атом водорода

167

В конечном выражении легко узнать известную из классической меха-ники формулу для центробежной силы. Квантовая механика, как это идолжно быть, воспроизводит на новом уровне результаты классической:теперь момент импульса стал оператором, но вошел на прежних правахв выражение для оператора полной энергии (гамильтониана).

Любой оператор коммутирует сам с собой, и так как оператор ква-драта момента вообще не зависит от радиальной переменной r,

то коммутирует с гамильтонианом из уравнения Шредингера .

Кроме того, оператор проекции момента импульса  коммутирует с и, стало быть, с гамильтонианом. Следовательно, выполняются класси-ческие законы сохранения квадрата и одной проекции момента импульса.Эти законы сохранения справедливы для любого центрально-симметрич-ного поля: специфика кулоновского взаимодействия пока нами не исполь-зовалась. Поэтому проекция и квадрат момента могут быть определеныодновременно с энергией и волновая функция стационарного состояниябудет зависеть от квантовых чисел l и m. Однако в уравнении Шре-дингера гамильтониан вовсе не зависит от оператора проекциимомента импульса. Это значит, что энергия состояния не будет зависетьот магнитного квантового числа m. Иными словами, в любом централь-но-симметричном поле имеется вырождение по т, кратность которогоравна 2l + 1. Мы уже знаем, что источником вырождения должна слу-жить та или иная симметрия. В классической физике движение частицыв центрально-симметричном поле всегда происходит по орбите, лежащейв одной плоскости. Но сама эта плоскость может быть произвольной взависимости от начального положения и скорости частицы. Ясно, чтозначение полной энергии частицы не зависит при этом от ориентацииплоскости орбиты в пространстве. Это и есть искомая симметрия, при-водящая к вырождению по магнитному квантовому числу.

В кулоновском поле (равно как и в гравитационном) имеется еще односпецифическое вырождение, приводящее к тому, что энергия системы независит и от квантового числа l. Вспомним опять классическую физику.В кулоновском поле финитное движение частицы совершается только поэллипсу. Возьмем в качестве аналогии искусственный спутник. Поме-стим его на каком-то расстоянии от Земли (т.е. зададим потенциаль-ную энергию) и придадим ему какую-то скорость (зададим кинетиче-скую энергию). Таким образом, мы задали полную энергию спутника.Но определена ли его орбита? Разумеется, нет! При той же полной энер-

168

Глава 31. Теория атома

гии направление скорости влияет на форму орбиты --- от прямой линии(вертикальное падение) при нулевом моменте импульса до максимальновозможного при данной полной энергии. Нулевой момент соответствуетчисто радиальным колебаниям сквозь центр притяжения, когда вовсе неткругового движения и эллипс вырождается в прямую линию (для спут-ника такое колебание невозможно, но микрочастицы --- иное дело). Мак-симально возможный момент импульса достигается в обратном случаечисто круговой орбиты, когда совсем нет радиального движения. Важно,что его величина зависит от полной энергии спутника.

Итак, классическая физика подсказывает нам следующие свойства ре-шений уравнения Шредингера:

    • Энергия электрона не должна зависеть от квантовых чисел l,т.

    • Квантовое число l должно пробегать ряд целых значений от нулевогодо максимального.

    • Максимальное значение l должно зависеть от энергии электрона.

 Вооружившись знанием классической механики, мы можем смело при-ступать к изучению квантовой. Теперь станут понятны свойства реше-ний уравнения Шредингера для атома водорода. Его решениями явля-ются волновые функции, нумеруемые тремя квантовыми числами: п, l, m.Про l и m уже много говорилось, ап --- знакомое нам по атому Бораглавное квантовое число, принимающее целые положительные значения.Разным наборам чисел п, l, m отвечают разные волновые функции, видкоторых нам сейчас не важен.

Задача 31.26. Волновая функция основного состояния электрона в атомеводорода имеет вид

                                                  

Найти вероятности W1 и W2 обнаружить электрон внутри сфер радиу-сами аB и 2аB.

Решение. Вероятность обнаружить электрон в элементе объема равна . Так как волновая функция основного состояния независит от направления радиус-вектора , а лишь от его величины r, томожно написать выражение для вероятности dWr обнаружить электрон вшаровом слое радиусом r и толщиной dr. Объем этого слоя равен 4r2 dr

31.3. Атом водорода

169

(площадь поверхности, умноженная на толщину). Именно им надо заме-нить элемент объема  в dW, чтобы получить dWr :

 dWr = 4r2| (r) | 2 dr .

 Теперь надо проинтегрировать вероятность dWr по всем значениямr от 0 до R, получив вероятность W (R) найти электрон внутри сферырадиусом R:

                                        

Интеграл берется точно, и в результате получаем:

                                                                             

откуда находим: W1 = W (аB) = 1 --- 5/е2 ? 0.323, W2 ?W(2 аB)

1 - 13/е4 ? 0.762.

Разность W2 --- W1 ? 0.439 дает вероятность найти электрон междусферами с радиусами аB и 2аB. Видно, что численно эта вероятностьимеет тот же порядок величины, что и вероятность W1. Зато вероятностьобнаружить электрон за пределами сферы радиусом 2аB заметно суще-ственно меньше: она равна, как нетрудно догадаться, 1 --- W2 ? 0.238.Иными словами, с вероятностью более 76% электрон в основном состоя-нии пребывает на расстоянии не более двух радиусов Бора. ¦

Задача 31.27. Найти электростатический потенциал, создаваемый ато-мом водорода в основном состоянии.

Решение. Возьмем любую точку на расстоянии R от ядра. Электро-статический потенциал в ней создается, во-первых, положительным за-рядом е ядра и, во-вторых, той частью заряда электрона, которая на-ходится внутри сферы радиусом R. Хорошо известно, что сфериче-ски симметричное распределение заряда не создает поля во внутреннихобластях. Поэтому часть электронного облачка, находящаяся дальшевыбранной точки, не внесет вклада в потенциал. Поскольку в уравне-нии вычислена вероятность W(R) нахождения электрона внутрисферы радиусом R, то отрицательный заряд внутри этой сферы равен

170

Глава 31. Теория атома

--- еW(R). Поэтому потенциал в точке R, создаваемый эффективным за-рядом q(R) = е(1 --- W(R)), имеет вид:

                         

На больших расстояниях потенциал убывает экспоненциально,то есть гораздо быстрее обычного кулоновского потенциала точечногозаряда. Это --- так называемый эффект экранировки: отрицательныйзаряд электрона компенсирует положительный заряд ядра. При R >0 потенциал переходит в обычный кулоновский потенциал: мыпроникли внутрь электронного облачка, где оно уже не экранирует зарядядра. ¦

Для энергии из уравнения Шредингера получается в точности такаяже формула, что и из теории Бора:

                                                 

Как видно, энергия действительно не зависит от квантовых чисел /,т.При этом, как следует из свойств решений уравнения , азимуталь-ное квантовое число l принимает целые значения от 0 до n --- 1. И этосвойство, угаданное нами на основе классической физики, воспроизвелосьв квантовой механике.

Удивительно, как квантовая механика, низвергнувшая столько клас-сических представлений, дает аналогичные результаты там, где вдело вступают свойства симметрии системы. Отсюда вывод: сим-метрия играет более важную роль, чем конкретные физические за-коны. Когда нибудь будут открыты новые законы, которые обобщати квантовую механику, и все теории, которые ныне находятся на пе-реднем крае науки. Но свойства симметрии системы проявят себятак или иначе.

Отличие квантовой механики от теории Бора --- более богатая структурауровней: состояние определяется тремя квантовыми числами, как и втрехмерном потенциальном ящике. Кстати, это не случайно. Три кван-товых числа в потенциальной яме и в атоме водорода --- отражение трех-мерности нашего пространства. Подсчитаем кратность вырождения, тоесть число различных состояний с той же энергией (главным квантовым

31.3. Атом водорода

171

числом п). При данном п число l пробегает значения от 0 до п --- 1 икаждому из них соответствует 2l + 1 значение m. Поэтому кратностьвырождения N равна

                                                                                                           

При п = 1 имеем N = 1, то есть основной уровень не вырожден. Прип = 2 кратность вырождения равна 4: уровень с l = 0 и три уровня сl = 1 и различными проекциями момента импульса т = ---1,0,+1. Прип = 3 кратность вырождения N = 9: один уровень с l = 0, три уровняс l = 1 и пять уровней (по числу проекций) с l = 2. Для классификацииуровней энергии по значению квантового числа l применяют условныеобозначения, позаимствованные из спектроскопии, где они появились ещедо создания теории атома:

l = 0 1 2 3 4 5 ...

символ s р dfg h...

Главное квантовое число ставится впереди символа. Примеры возмож-ных состояний:

 1s, 2s, 2р, 3s, 3р, 3d, 4s, 4р, 4d, 4f еtс.

 При переходе электрона с уровня на уровень излучается фотон, унося-щий собственный угловой момент, равный h. Следовательно, разрешенытолько переходы с изменением l на единицу: возникает правило от-бора l = 1. Это значит, что в атоме водорода допустимы переходыпр >1s, пs > 2р, еtс, приводящие к тем же спектральным сериям, чтои теория Бора. Более богатая структура уровней не проявляется пока вбольшем разнообразии атомных спектров из-за вырождения.

Говоря о вырождении уровней, мы имели в виду водородоподобныйатом. В более сложных атомах или в присутствии внешних электро-магнитных полей вырождение, как говорят, снимается и появляется за-висимость энергии от чисел l,т. Любая не кулоновская центрально-симметричная поправка к потенциальной энергии приведет к зависимо-сти уровней энергии от l (наблюдается в щелочных металлах). В клас-сической физике такая поправка к обычному закону притяжения (напри-мер, планеты к Солнцу) превращает эллиптические орбиты в незамкну-тые кривые. Обращаясь по таким орбитам, планета как-бы движетсяпо обычному эллипсу, который дополнительно вращается как целое, пре-цессирует в той же плоскости. Подобный эффект --- вращение перигелия

172

Глава 31. Теория атома

Меркурия, предсказала общая теория относительности. Новое движениеприводит к дополнительный энергии вращения, зависящей от l. В ре-зультате энергия уровня 2s перестанет совпадать с энергией уровня 2ри т.п.

Любое не центрально-симметричное поле (например, магнитное) сни-мет вырождение по ш. В классической физике магнитное поле вызываетпрецессию плоскости вращения вокруг направления поля и также по-явление из-за этого вращения дополнительной энергии. Сказанное можносформулировать в виде общего вывода:

Всякое дополнительное взаимодействие, нарушающее симметрию си-стемы, снимает соответствующее ей вырождение уровней энергии.На эксперименте снятие вырождения проявляет себя в расщеплениипрежних спектральных линий на несколько компонентов.

    • Спин электрона и тонкая структура спектров

 Дальнейшее исследование атомных спектров показало, что многие спек-тральные линии имеют два близких компонента. Так, еще в 1887 г.А. Майкельсон обнаружил расщепление ---линии серии Бальмера в водо-роде (порождаемой переходом 3р > 2s): она оказалась состоящей из двух

линий со средней длиной волны 6563 Е и разностью длин волн 0.14 Е (т.е.относительная величина расщепления порядка 10-5). Были обнаруженыи линии, расщепленные на 3, 4 и более компонентов. Расщепление линий,как мы теперь понимаем, означает расщепление энергетических уровнейатома: у них появляется, как говорят, тонкая структура. Значит, су-ществует неучтенное взаимодействие. Мы говорили, что расщеплениелиний появляется, например, когда наложенное внешнее поле нарушаетсимметрию системы. А здесь неучтенное взаимодействие проявляется вотсутствии внешних полей, то есть оно должно быть связано с какими-товнутренними свойствами атома.

Оказалось, что здесь действительно проявились внутренние свойства,но не атома в целом, а электрона. В 1925 г. С. Гаудсмит и Дж. Улен-бек выдвинули гипотезу спина электрона: они предположили существо-вание у электрона собственного момента импульса, не связанного с ор-битальным движением. Сначала спин представляли себе как верчение(англ, spin) электрона вокруг собственной оси (аналог суточного враще-ния Земли). Потом осознали, что ``верчение"" нельзя понимать буквально:

31.4. Спин электрона и тонкая структура спектров

173

численные оценки давали линейную скорость верчения, превышающуюскорость света.

    • Сейчас под спином понимается собственный момент количества дви-жения электрона как врожденное квантовое свойство. Его существо-вание остается загадкой, если находиться только в рамках квантовоймеханики Гейзенберга-Шредингера. Естественное объяснение спинполучил только в релятивистской квантовой теории Дирака, соеди-нившей теорию относительности с квантовой механикой.

 Из опытов следовало, что электрону надо приписать спиновое квантовоечисло s = 1/2, имеющее те же свойства, что и квантовое число /: соб-ственные значения оператора квадрата спина равны h2s(s + 1) = 3h2/4, апроекция спина на какую-то ось пробегает через единицу все значения отмаксимального до минимального (для электрона проекция спина sz = /h,где а принимает лишь значения = 1/2).

Откуда же взялось расщепление спектральных линий? Попытаемсяпонять это с помощью полуклассических рассуждений. В классическойфизике любое вращение электрического заряда создает магнитное поле.Вращающийся по орбите классический электрон можно представить каквиток с током силой I, охватывающий площадь S, т.е. как диполь смагнитным моментом  = IS (эту формулу знал еще Ш. Кулон). Клас-сическая оценка: электрон на орбите радиусом R и скоростью  имеетпериод обращения . Возьмем какую-нибудь точку на орбите.За время Т через нее проходит заряд е, то есть сила тока по определе-нию равна I = е/Т = е/2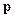R. Кроме того, электрон имеет орбитальныймомент L = тeR, так что ток можно выразить через орбитальный мо-мент, исключив скорость электрона: I = еL/(2тетR2) = еL/(2теS), гдемы ввели площадь ``витка"" S= R2. Тогда орбитальный магнитныймомент, создаваемый электроном, равен  = еL/2mе. Заменим теперь всоответствии с правилами квантования 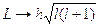 и получим выра-жение для орбитального магнитного момента, которое может быть вы-ведено и более строго:

                                                                                                             

Отсюда следуют выводы:

    • Естественная единица для магнитных моментов в микромире --- так

 174

Глава 31. Теория атома

называемый магнетон Бора

                                                                 

    • Проекция магнитного момента на любую ось всегда должна быть це-лым кратным магнетона Бора:  . Теперь понятно, почему

 квантовое число m названо магнитным.

    • Отношение магнитного момента к орбитальному моменту количе-ства движения равно е/2mе (его называют гиромагнитным отноше-нием) .

Эксперименты показали, что электрон обладает двойным магнетиз-мом: его собственный магнитный момент, связанный со спином, равен, то есть гиромагнитное отношение для него оказалосьв два раза большим (е/те). Это --- лишнее доказательство, что электроннельзя представлять себе как заряженный шарик, вращающийся вокругсобственной оси: в таком случае должно было бы получиться обычноегиромагнитное отношение. Для проекции собственного магнитного мо-мента имеем sz = 2B и поскольку  = 1/2, то sz = B. В итогедля проекции спинового магнитного момента снова получились целыекратные магнетона Бора как и для орбитального движения. По какой-топричине природа предпочитает иметь дело с целым магнетоном Бора,а не с его частями. Поэтому полуцелое значение собственного моментаколичества движения она компенсирует двойным гиромагнитным отно-шением.

Теперь можно понять, почему наличие у электрона собственного маг-нитного момента приводит к появлению какого-то неучтенного до сих порвзаимодействия. Для этого опять перейдем на полуклассический язык.Орбитальное движение электрона создает магнитное поле, которое дей-ствует на собственный магнитный момент электрона. Подобным образоммагнитное поле Земли воздействует на стрелку компаса. Энергия этоговзаимодействия сдвигает энергетические уровни атома, причем величинасдвига зависит, вообще говоря, от спинового и орбитального моментовколичества движения.

Взаимодействие спинового и орбитального магнитных моментов при-водит к снятию вырождения и к расщеплению спектральных линий.

31.4. Спин электрона и тонкая структура спектров

175

Задача 31.28. Оценить расщепление уровней энергии вследствие взаи-модействия спинового и орбитального магнитного моментов электрона ватоме водорода.

Решение. Круговой виток радиусом R с током силой I порождает вцентре магнитное поле В = 0I/2R. В этой главе было показано, чтовращающийся по орбите электрон можно представить как виток с токомI = еL/(2mR2) ? B/(R2). Здесь для оценки мы положили L ? h.Тогда получаем для магнитного поля, создаваемого орбитальным дви-жением электрона в атоме величину порядка В ? 0B/(2R3). Энергиявзаимодействия собственного магнитного момента электрона с этим маг-нитным полем равна по порядку величины:

                                                    

Для оценки положим R равным боровскому радиусу первой орбиты ощ.Подставляя сюда выражения для аВ и В и учитывая, что 00 = 1/с2,получаем оценку сдвига энергетических уровней:

                                                                                       

где --- введенная выше постоянная тонкой структуры. Энергия первогоуровня атома водорода, как известно, равна Е = 2тс2 /2, так что можно переписать как Е ? 2Е. Поскольку  ? 1/137, а Е = 13.6 эВ,то Е ? 0.72 мэВ, а относительный сдвиг уровней Е = Е /Е ? 2 ? 5 10-5, что соответствует экспериментальным данным. ¦

Это есть оценка (не расчет) искомого расщепления уровней. В сущ-ности, расщепление уровней --- это релятивистский эффект: по Борускорость электрона на первой орбите  ? с и Е ? (/с)2. Поэтомуне удивительно, что до конца свойства спина могут быть поняты тольков релятивистской квантовой теории. Мы не ставим себе такую задачу,но просто будем учитывать наличие у электрона этого удивительногосвойства.

Прямое экспериментальное доказательство существования спина элек-трона было дано в опыте Штерна-Герлаха в 1922 г. Идея опыта состоитв том, что в магнитном поле, неоднородном по оси z, на электроны дей-ствует смещающая сила, направленная вдоль поля.

Происхождение этой силы проще уяснить сначала на примере элек-трического диполя, помещенного в электрическое поле. Электрический

176

Глава 31. Теория атома

диполь представляет собой пару противоположных зарядов е, располо-женных на малом расстоянии l друг от друга. Величина электрического

момента определяется как , причем вектор  считается направлен-ным от отрицательного заряда к положительному.

Пусть положительный заряд находится в точке , а отрицательный ---в точке , так что . Пусть диполь помещен в электрическоеполе с напряженностью . Найдем силу, действующую на диполь. Наположительный заряд действует сила , на отрицательный ---. Результирующая сила

                                          

Так как расстояние между зарядами мало, то поле в точке расположенияотрицательного заряда можно приближенно записать как

                                              

Подставляя это разложение в выражение для силы Е, находим

.

 Если поле однородно ( не зависит от ), то на заряды диполя действуютравные и противоположно направленные силы и результирующая силаравна нулю, как и следует из уравнения . Как известно, такаяпара сил не смещает диполь (который в целом электрически нейтрален),но лишь поворачивает его вдоль поля (магнитный аналог --- стрелкакомпаса). В неоднородном же поле результирующая сила отлична отнуля. В частном случае, когда поле зависит только от координаты 2,в уравнении отлична от нуля лишь производная по 2:

                                                        

где dz --- проекция электрического момента на ось z. Неоднородное полестремится втянуть диполь в область, где оно сильнее.

Магнитных зарядов не существует, но магнитный диполь реализуетсявитком с током и его свойства аналогичны свойствам электрическогодиполя. Поэтому в формуле надо заменить электрическое полена магнитное, электрический момент --- на магнитный и написать длясилы, действующей на электрон в опыте Штерна-Герлаха, аналогичноевыражение:

                                                       

31.4. Спин электрона и тонкая структура спектров

177

Схема опыта: пучок атомов пролетает сквозь неоднородное магнит-ное поле, направленное поперечно к скорости атомов. Сила, действую-щая на магнитные моменты атомов, отклоняет их. Соответственно воз-можным значениям проекции магнитного момента на направление поля,первоначальный пучок расщепляется на несколько пучков. Если пол-ный магнитный момент атома определяется только спином электрона, топервоначальный пучок расщепится на два. Для многоэлектронных ато-мов расщепленных пучков может быть больше. Для своего экспериментаШтерн и Герлах использовали серебро, которое испарялось в электриче-ской печке. Численные значения расщепления составляли доли миллиме-тра. Авторы подчеркнули в своих выводах, что неотклоненных атомов небыло зарегистрировано. Ниже мы увидим, что это --- специфика опытовс элементами первой группы.

Главный результат опытов Штерна и Герлаха --- прямое эксперимен-тальное доказательство квантования направления магнитного моментаатомов. Согласно классической физике, первоначальный пучок должен нерасщепиться, а размазаться в соответствии с произвольностью проекциимагнитного момента на направление магнитного поля. Соответственно,на экране за прибором вместо двух раздельных линий, оставленных ато-мами серебра, должна была бы наблюдаться размытая полоска.

Задача 31.29. Узкий пучок атомов со скоростью  и массой т пропус-кается через поперечное неоднородное магнитное поле, в котором на нихдействует сила Fz (рис. 31.3). Протяженность поля l1, расстояние от маг-нита до экрана l2. Определить отклонение следа пучка атомов на экранеот его положения при выключенном магнитном поле.

Решение. Здесь мы имеем дело с задачей классической механики, ко-торая позволяет подготовиться к количественному рассмотрению опытаШтерна-Герлаха. Время пролета атома через магнит равно t = l1/.Все это время на атом действует поперечная сила ЕД придающая емупоперечное ускорение а = Fz/т. За время пролета атом отклонится нарасстояние s1 = аt2/2=Fz/(2т2) и приобретет поперечную скорость. Это значит, что из магнита атом вылетает подуглом  к первоначальному направлению движения, причем tg = .Следовательно, при пролете расстояния l2 до экрана атом отклонитсяеще и на расстояние . Складывая

178

Глава 31. Теория атома

Рис. 31.3: К задаче (31.29.) об отклонении атомов магнитным полем: ОА = s1, АВ =

s2, ОВ = s.

 отклонения s1 и s2, получаем искомое отклонение следа атома на экране:

                                                                                                           

Часто в задаче стоит вопрос об отклонении пучка атомов при выходе измагнита. В таком случае надо положить l2= 0 в полученной формуле. ¦

Задача 31.30. Узкий пучок атомов серебра при прохождении магнит-ного поля с неоднородностью дВ/дz = 1 кТл/м протяженностью l1 =4 см расщепился на два пучка. Экран для наблюдения установлен нарасстоянии l2 = 10 см, скорость атомов = 0.5 км/с. Определить рас-стояние b между компонентами расщепленного пучка на экране.

Решение. Заполненные оболочки дают нулевой вклад в магнитный мо-мент атома. Атом серебра имеет один валентный электрон, и потомуего магнитный момент равен магнитному моменту электрона. В неод-нородном поле на атом действует сила  где B --- магнетон

Бора. Знаки  соответствуют двум возможным направлениям магнит-ного момента электрона и потому пучок расщепляется на два. На экраненаблюдаются две полоски, находящиеся на расстоянии b друг от друга.Если в формулу подставить выражение для силы Fz, то получимдва отклонения s, отличающиеся знаком. Поэтому искомое расщеплениеb = 2s. В результате приходим к выражению:

                                                

Массу атома серебра легко найти по таблице Менделеева: молярнаямасса атомная масса М = 107.868 г/моль. Чтобы найти массу, надо

31.5. Векторная модель атома

179

М разделить на число Авогадро: т = 107.868 10-3/6.02 10-23 = 1.7910-25 кг. Подставим теперь в численные значения:

                 

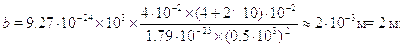
Такое расщепление вполне наблюдаемо в опытах.

    • Векторная модель атома

 Обсудим качественные изменения, вносимые спином электрона в теориюатома. Полный момент импульса складывается теперь из орбитальнойи спиновой частей. Возникает новое квантовое число j принимаю-щее два значения (при l = 0 полный момент импульса j = 1/2).Эти значения соответствуют двум случаям, когда спин параллелен и ан-типараллелен орбитальному моменту импульса. Необходимо ввести но-вые обозначения уровней: добавляется индекс, указывающий величинуполного момента импульса: уровни обозначают пxj где п --- главноеквантовое число, a x --- прежний буквенный символ для обозначения ве-личины азимутального квантового числа l. Свойства полного моментате же, что и у орбитального и спинового моментов. Как следствие но-вого вида взаимодействия возникает более богатая структура атомныхспектров, наблюдавшаяся на опыте. Проиллюстрируем это на примерепервых возбужденных уровней атома водорода (таблица 31.1).

Энергия уровней уже выражается не формулой Бора, но содержит по-правки относительной величины 2. Мы не станем ее приводить, ноотметим характерное свойство: в отсутствие внешних полей энергия по-прежнему не зависит от орбитального момента l, но лишь от полногомомента импульса j. Значит, уровни 2s1/2 и 2р1/2 вырождены (их энер-гии совпадают). Уровень 2р3/2, как оказывается, лежит чуть выше.

Состояния многоэлектронных атомов классифицируются подобным обра-зом. Если  --- суммарный орбитальный момент всех электронов, а  ---их суммарный спиновый момент, то полный момент системы определя-ется как. Соответственно и обозначается это состояние как2S+1XJ. Под X понимается тот же буквенный символ, обозначающий зна-чение орбитального момента количества движения (только в этом слу-чае используется заглавная буква). Верхний левый индекс равен числуспиновых состояний (для одиночного электрона в нем не было необходи-мости, так как его спин всегда равен 1/2).

180

 Глава 31. Теория атома

 Таблица 31.1: Схема нижних уровней атома водорода

Итак, пусть дано состояние 2S+1XJ. Встает вопрос: чему равен маг-нитный момент системы ? Ясно, что он направлен вдоль полного мо-мента количества движения , а его размерность определяется магнето-ном Бора B- Тогда

                                                         

                                                                                                           

Для гиромагнитного отношения (обобщение аналогичной величины, свя-занной с орбитальным и спиновым моментами) можно тогда написатьвыражение вида еg/2те. Коэффициент пропорциональности g называ-ется множителем Ланде или просто (g-фактором. Для орбитального дви-жения g = 1, для спинового магнитного момента g = 2. Задача о магнит-ном моменте атома сводится к нахождению зависимости g от квантовыхчисел J, L и S.

Ответ можно получить с помощью простой полуклассической модели,получившей название векторной модели атома. Сначала возведем в ква-драт уравнение, связывающее 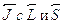: . Квадратымоментов можно выразить через соответствующие квантовые числа поуже известным нам правилам. Находим тогда выражение для скалярного

31.5. Векторная модель атома

181

произведения

                                    

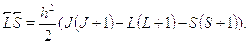
Полный магнитный момент складывается из магнитного момента, со-здаваемого суммарным орбитальным моментом количества движения,и суммарного спинового магнитного момента. Но спин, как уже гово-рилось, обладает двойным магнетизмом. Поэтому с учетом уравнения можно записать:

Сокращая общий множитель B и умножая обе части на ,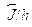в правойчасти  заменен на ), получаем:

Если подставить сюда выражение для скалярного произведения, то получим окончательный ответ:

Убедимся, что эта формула воспроизводит уже известные результаты.Если полный спиновый момент равен нулю, то полный момент совпа-дает с орбитальным. Подставляя в значения S = 0, J = L,получаем g = 1, как и должно быть для магнитного момента, создава-емого чисто орбитальным движением электронов. В обратном случаенулю равен орбитальный момент и полный момент количества движе-ния равен спиновому. Подставляя в значения L = 0, J = S, на-ходим g = 2 в полном согласии с двойным магнетизмом спинового мо-мента. Именно такой случай реализуется для элементов первой группы вопыте Штерна-Еерлаха. Упоминалось, что для сложных атомов (напри-мер, серы) расщепление пучков будет более сложным. Теперь мы можемпредсказать результат количественно. Основное состояние серы 3Р2, тоесть S=1, L=1, J = 2. Из формулы для множителя Ланделегко получаем g = 3/2, так что магнитный момент атома равен

                   

                                      

                                                        

182

Глава 31. Теория атома

Проекция магнитного момента на ось z

                                                       

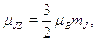
где тJ (проекция полного момента количества движения) принимаетпять различных значений в соответствии с правилами квантования мо-мента: тJ = 2, 1, 0. Теперь, используя результаты задач в концеглавы, можно рассчитать расщепление пучка атомов серы в опыте Штерна-Герлаха. Ясно, что пучок расщепится на пять компонентов, причем однаиз них (тJ = 0) не будет отклоняться магнитным полем.

    • Принцип Паули и валентность элементов

 Мы видели, что орбитальный момент импульса характеризуется азиму-тальным квантовым числом l, принимающим целые значения. Собствен-ный спиновый момент характеризуется спиновым квантовым числом s,равным 1/2 для электрона. Спин --- фундаментальное квантовое свой-ство всех элементарных частиц. В соответствии со значением спиновогоквантового числа 5 частицы делятся на два класса: бозоны (целые s) ифермионы (полуцелые s). Другие значения s науке не известны. При-меры фермионов: электрон, мюон, нейтрино, кварки, частицы из трехкварков (протон, нейтрон). Пример бозонов: фотон, недавно открытыеW и Z частицы из двух кварков (-мезоны и др.).

    • Бозоны и фермионы --- это не имена собственные каких-то частиц,а названия целых семейств. Каждая микрочастица принадлежитодному из них и поменять принадлежность уже не в состоянии. Втеории элементарных частиц замечено, что из фермионов построеновещество, а бозоны переносят фундаментальные взаимодействия.

 Если собрать вместе несколько бозонов, то они не мешают друг другузанять низшее энергетическое состояние и, следовательно, все там ока-жутся. Поведение коллектива фермионов регулируется принципом Па-ули:

    • два одинаковых фермиона не могут находиться в одном и том жесостоянии.

 В применении к атому принцип Паули запрещает двум электронам иметьодинаковый набор квантовых чисел: состояния электронов должны от-личаться значением хотя бы одного из них. Если бы принципа Паули

31.6. Принцип Паули и валентность элементов

183

не существовало, то у всех атомов в основном состоянии все электронынаходились бы на нижнем энергетическом уровне и атомы различныхэлементов были бы до ужаса похожи друг на друга. Таким образом,известная нам химия, все разнообразие элементов и их свойств (в част-ности, гамма вкусовых ощущений, отличающая, скажем, вино от сыра)--- следствия принципа Паули. До сих пор мы в основном рассматривалитолько атом с одним электроном. Станем добавлять лишний электрон и,соответственно, увеличивать на единицу заряд ядра. Иными словами, со-вершим прогулку по таблице Менделеева. Введем понятия оболочки каксовокупности уровней с одинаковыми главными квантовыми числами п иподоболочки (уровни данной оболочки с одинаковыми l). Традиционныеобозначения

п = 1, 2, 3, 4, ...

символ К, L, М, N ....

Число уровней в оболочке мы фактически уже подсчитали: оно равнократности вырождения по т и /, умноженной на 2 в соответствии с двумявозможными направлениями спина электрона. Таким образом, оболочкаможет вместить 2п2 электронов, а подоболочка --- 2(2l + 1) электронов(число различных значений m, удвоенное по той же причине). Состоя-ния в атоме различаются квантовыми числами п, l, т и  (проекцияспина). По принципу Паули лишь один электрон может иметь данныйконкретный набор квантовых чисел.

Напоминание: три квантовых числа п, l и т отражают трехмер-ность пространства, --- внутренние свойства электрона.

Порядок замещения уровней в многоэлектронных атомах определяетсяэнергией уровней с учетом влияния заполненных оболочек. Нижние обо-лочки частично экранируют заряд ядра, что ведет к некулоновскомуполю для высших оболочек. Этим объясняется зависимость энергииуровней от квантового числа l. Чем больше l, тем дальше находитсяэлектрон от ядра и тем слабее его связь с ядром, т.е. такой уровеньлежит выше. При больших моментах (состояния d, f и т.п.) уровеньблизок или даже выше s-подуровней следующей оболочки. В целом за-полнение идет в таком порядке (случаются небольшие отклонения):

1s | | 2s, 2р | | 3s, 3р | | 4s, 3d, 4р | | 5s, 4d, 5р | | 6s, 4f, 5d, 6р | | еtс.

В этом ряду знаком | | отделены периоды таблицы Менделеева. В соот-ветствии с полученными формулами для числа уровней в зависимости от

184

Глава 31. Теория атома

п и /, / период содержит 2 элемента, II и III --- по 8, в IVиV --- по 18элементов. Здесь ``вклиниваются"" заполнения d-подоболочек (по 10 эле-ментов --- переходные металлы). В VI периоде добавляется заполнение/-подоболочки (14 элементов --- лантаниды) и т.д.

Химические свойства зависят в основном от строения внешней элек-тронной оболочки (валентных электронов). Отсюда и вытекает перио-дичность повторения свойств элементов. Так, у благородных газов за-полнены внешние 5--- и р---подоболочки из 8 электронов. У элементов пер-вой группы (щелочные металлы) на внешней оболочке имеется всего одинэлектрон, а галогенам (VII группа) не хватает одного электрона для за-полнения внешней р---подоболочки. Все эти рассуждения хорошо знакомыпо курсу химии, но они носят качественный характер. Как известно,валентность элемента определяется не столько количеством электронов,сколько степенью легкости, с которой их можно вырвать из атома. По-нятно, что внешние электроны оторвать легче, но хотелось бы получитьхоть какой-нибудь количественный критерий. Таким критерием можетслужить так называемый потенциал ионизации --- энергия, которую не-обходимо затратить, чтобы удалить электрон из атома. Расчет сложныхатомов непрост, но в целом таблица Менделеева объясняется квантовоймеханикой. Мы ограничимся лишь самыми простыми атомами и точ-ные расчеты заменим количественными оценками. Экспериментальныерезультаты представлены на рис. 31.4.

Эффективный заряд ядра, оценки потенциала ионизации и за-кон Мозли

 Мы в деталях изучили энергетические уровни водородоподобных атомов,описываемые формулой Бора

                                                    

Для более сложных систем со многими электронами эта формула неверна,но мы будем ее использовать, вводя поправку на экранировку ядра элек-тронами путем замены заряда ядра 2 на некий эффективный заряд 2е.Большой точности сравнения с экспериментальными данными так не до-биться, но мы удовлетворимся совпадением по порядку величины.

Водород Заряд ядра Z = 1, экранировки нет, в основном состояниип = 1. Энергия основного уровня Е1 = ---13.6 эВ, минимальная энер-гия электрона, вырванного из атома, равна нулю. Следовательно,

31.6. Принцип Паули и валентность элементов

185

Рис. 31.4: Потенциал ионизации для элементов от водорода до урана. Ясно видна пери-одичность свойств элементом. Пики потенциала ионизации случаются для благородныхгазов, минимумы --- для щелочных металлов.

 ионизационный потенциал U --- это абсолютное значение энергииосновного состояния: U = 13.6 эВ. Это значение будет служить намориентиром, позволяющим не заблудиться в энергетической шкалемикромира.

Положительный ион гелия Ион Не+ отличается от водорода толькоудвоенным зарядом ядра: Z = 2. Отсюда U = 13.6 х 4 = 54.4 эВ.

Гелий Нейтральный атом гелия в основном состоянии имеет два элек-трона на нижней оболочке (п = 1), отличающиеся проекциями спи-нов. Представим себе такую картину. Когда второй электрон нахо-дится дальше от ядра, чем первый, то заряд ядра от него экраниру-ется и равен (с его ``точки зрения"") единице. Когда же второй элек-трон располагается к ядру ближе первого, то ``видимый"" им зарядядра равен двум. Оба электрона равноправны, так что описанныеситуации равновероятны. Поэтому для оценки эффективного зарядаядра мы возьмем среднее арифметическое: Zeff = (1 + 2)/2 = 3/2.Конечно, электрон не может полностью экранировать ядро от своегопартнера. Конечно, надо принять во внимание энергию кулоновскогоотталкивания электронов. И все же получающаяся оценка не столь

186

Глава 31. Теория атома

плоха:

 = 30.6 эВ.

Эксперимент дает U = 24.6 эВ.

Бросается в глаза огромная величина ионизационного потенци-ала у гелия (самый большой в таблице Менделеева). Инертностьгелия --- прямое следствие этого факта.

Дважды ионизованный атом лития Li++ Водородоподобная системас Z = 3. Поэтому U = 13.6 х 9 = 122.4 эВ.

Ион лития Ион Li+ подобен атому гелия, но для него эффективный за-ряд ядра на единицу больше: Zeff = 5/2. Отсюда U ? 13.6  (25/4) =85 эВ. Эксперимент дает U = 81 эВ.

Литий Третий электрон в нейтральном атоме лития располагается навторой оболочке --- уровне с п = 2. По этой причине два внутреннихэлектрона почти полностью экранируют от него две единицы зарядаядра: Zeff ? 1. Отсюда U ? 13.6/4 ? 3.4 эВ. Эксперимент дает

    • Эти оценки очень показательны: насколько легче (в сравнениис водородом) оторвать от лития один электрон и как трудноудалить последующие. Поэтому литий --- одновалентен.

 Бериллий Ионы Ве+++ и Ве++ аналогичны водороду и гелию и имеютогромные потенциалы ионизации. Ион Ве+ похож на литий, но унего на единицу больше эффективный заряд ядра, ``видимый"" тре-тьим электроном: Zeff = 9/4. Получаем U ? 13.6(81/16)(1/4)

= 17.2 эВ. Эксперимент дает 18.2 эВ. Это значение не намногобольше потенциала ионизации атома водорода и заведомо много меньшепотенциала ионизации иона Ве++. В нейтральном атоме Ве на вто-рой оболочке помещаются два электрона. Система похожа на ионLi-, но эффективный заряд ядра на единицу больше: Zeff ? 3/2.Отсюда U ? 13.6(9/4)(1/4) = 13.6(9/16) = 7.7 эВ. Эксперименталь-ное значение U = 10.4 эВ.

Отсюда вывод: поскольку первые два электрона вырвать изатома бериллия гораздо легче, чем последующие, то Ве --- двух-

U = 5.4 эВ.

валентен.

31.6. Принцип Паули и валентность элементов

187

Понятие эффективного заряда ядра полезно также при рассмотрениисвойств так называемого характеристического рентгеновского излуче-ния, возникающего при переходе внешних электронов на свободное ме-сто на внутренних оболочках. Как мы выяснили, для электронов на Коболочке Zeff ? Z --- 1/2. Пример: для СиZ = 29 и Zeff ? 28.5. Припереходе внешних, далеких от ядра электронов с энергией, почти рав-ной нулю, испускается фотон с энергией Е ? 13.6  2 ? 11000 эВ.Длина волны такого фотона  = с/ = hс/Е = 1.12 Е. В 1913 г. былустановлен закон Мозли, связывающий частоту  характеристическогорентгеновского излучения элемента и его атомный номер Z:

где Ry --- постоянная Ридберга, с --- скорость света, п --- главное кван-товое число оболочки, на которую совершается переход, а п --- некаяпостоянная. В этом законе легко теперь увидеть проявление экранирова-ния ядра, то есть влияние на отдельный электрон атома всех остальныхэлектронов. Исторически закон Мозли окончательно подтвердил, чтосвойства элемента зависят от Z, а не от атомной массы. Это устранилопоследние сомнения в правильности расположения элементов в периоди-ческой системе.

Электронная конфигурация атомов

 Для атома любого элемента мы можем указать его электронную кон-фигурацию. Теперь познакомимся с двумя правилами, позволяющимиузнать для основного состояния каждого атома значение его суммарныхмоментов: спинового S, орбитального L и полного J.

    • Наименьшей энергией обладает атом с наибольшим возможным приданной электронной конфигурации значением 5 и наибольшим воз-можным при этом S значением L(правило Хунда).

    • Если в незаполненной подоболочке атома находится не более поло-вины максимально возможного для нее числа электронов, то J =| L --- S| . Если же подоболочка заполнена более, чем наполовину, то

J = L + S.

Правило Хунда является эмпирическим (т.е. не выведенным из теории,а установленным экспериментально); второе правило выводится из него

188

Глава 31. Теория атома

и из полученной выше формулы для скалярного произведения  .Для облегчения применения правила Хунда полезно запомнить, что:

1) надо рассматривать только незаполненную электронную подоболочку,так как моменты электронов в заполненных подоболочках взаимнокомпенсируются;

2) значения S и L одинаковы для двух подоболочек, из которых однаимеет столько электронов, сколько не хватает для заполнения дру-гой.

Для примера применения указанных правил рассмотрим атом серы. Егоатомный номер Z = 16 и, следовательно, электронная конфигурацияимеет вид 1s22s22рб3s23р4:. Индексы справа вверху обозначают числаэлектронов в указанных состояниях. Видим, что незаполненной остаетсятретья оболочка, на которой находятся четыре электрона с орбиталь-ными моментами, равными единице. При данном L = 1 согласно прин-ципу Паули параллельными могут быть лишь спины трех электронов,отличающихся значениями m = ---1,0,1. Спин четвертого электронадолжен быть направлен в противоположную сторону, и потому макси-мально возможное значение суммарного спина для данной конфигурацииравно S = 3/2 --- 1/2 = 1.

При этом значении 5 сумма проекций орбитальных моментов элек-тронов с одинаково направленными спинами равна нулю, следовательно,максимально возможное значение проекции суммарного орбитального мо-мента определяется четвертым электроном и равна единице. ПоэтомуL = 1. Так как внешняя подоболочка заполнена более чем наполовину,то J = L + S = 2. Мы пришли к выводу, что основным состоянием атомасеры является 3Р2.

Для сравнения найдем основное состояние атома кремния (Z = 14).От атома серы он отличается тем, что на внешней подоболочке у негонаходятся два, а не четыре р-электрона. Для ее заполнения не хватает че-тырех электронов, то есть столько, сколько их имеется у серы. Поэтомудля атома кремния получаем те же значения S = 1 и L = 1. Внешняяподоболочка заполнена менее чем наполовину, откуда J = | L --- S| = 0.Поэтому основным состоянием кремния является 3Р0.

31.6. Принцип Паули и валентность элементов

189

Контрольные вопросы

    • Сформулируйте правила квантования момента импульса и проекции момента навыделенную ось.

    • Какими квантовыми числами описывается состояние электрона в атоме? От какихквантовых чисел зависит энергия электрона?

    • Какова кратность вырождения энергетического уровня в атоме водорода?

    • Какова размерность волновой функции электрона в СИ?

    • Чему равен потенциал ионизации атома водорода? Какова зависимость энергииэлектрона от главного квантового числа?

    • В каких аспектах волновая теория атома совпадает с теорией Бора, а в каких этитеории различны?

    • Перечислите свойства электрона, связанные с наличием у него спина.

    • Что такое магнетон Бора? Чему равно гиромагнитное отношение для орбиталь-ного движения и для спина?

    • Опишите схему опыта Штерна-Герлаха. От чего зависит число компонентов, накоторые расщепляется пучок атомов в этом опыте?

    • Почему направление магнитного момента электрона противоположно направле-нию его спина?

    • Сформулируйте принцип Паули. Что такое электронные оболочки и подоболочкив атоме? Объясните роль принципа Паули в повторяемости (периодичности)свойств химических элементов.

    • Как связан потенциал ионизации с валентностью элемента? Почему электронтруднее удалить из атома неона, чем из атома натрия?

    • Предположим, что никакого спина у электрона не существует, так что его со-стояние в атоме определяется лишь тремя квантовыми числами п,1,т. Какиепоследствия это имело бы для таблицы элементов Менделеева и нашей жизни?

    • Предположим, что спин электрона равен 3/2. Какой элемент играл бы тогда рольгелия --- первого из группы благородных газов? Какой элемент был бы вторым вэтой же группе?

    • * Найти основное состояние атома фосфора (Z = 15).

 Глава 32

Физическая природа химическойсвязи

32.1 Молекулы

 Атомы представляют собой связанные электрическими силами системыядер и электронов. В свою очередь, атомы под действием тех же силв определенных условиях могут объединяться в молекулы. Первона-чально химия предполагала существование специфических ``химическихсил"" для объяснения образования молекул из атомов, а также химиче-ских реакций между атомами или молекулами. Однако таких ``химиче-ских сил"" не существует: образование молекул обусловлено обычнымиэлектрическими (кулоновскими) силами взаимодействия между заряжен-ными частицами, т.е. электронами и ядрами, из которых состоят атомы.Но механизм образования молекул можно понять только на основе кван-товой механики. Для простоты ограничимся рассмотрением простей-ших двухатомных молекул. Силы, удерживающие атомы в молекуле,вызваны взаимодействием внешних электронов, а электроны внутреннихоболочек при объединении атомов в молекулы остаются в прежних состо-яниях. Различают два вида связи между атомами в молекуле: ионную(гетерополярную) и ковалентную (гомеополярную).

Ионная связь

 Этот вид химической связи обусловлен переносом валентных электроновс одного атома на другой и кулоновским притяжением образовавшихсяионов. Иными словами, ионная связь осуществляется в том случае, ко-гда электроны в молекуле можно разделить на две группы, каждая изкоторых все время находится около одного из ядер. Электроны разде-

190

32.1. Молекулы

191

ляются так, что около одного из ядер образуется избыток электронов, аоколо другого --- их недостаток, т.е. молекулу можно представить какобразование, состоящее из отрицательного и положительного ионов, при-тягивающихся друг к другу (например, молекула NaCl состоит из ионовNa+ и Cl-

Для описания ионных молекул еще до создания квантовой механики суспехом применялись полуэмпирические способы расчета энергии связи,основанные на классической электростатике. Пусть, например, мы имеемдело с молекулами типа КСl, NaCl и т.п. Обозначим через Um ионизаци-онный потенциал щелочного металла, а через Uh --- сродство галогена кэлектрону. В начальном состоянии имеем два нейтральных атома К и Сl,разнесенные на бесконечно большое расстояние. Попытаемся мысленнопостроить из них молекулу. Затрачивая энергию Um, мы отрываем элек-трон от металла и переносим его на галоген. При присоединении элек-трона к последнему выделится энергия Uh, так что энерговыделение наэтом этапе составляет Uh ---Um. Далее сближаем образованные нами ионыдо равновесного расстояния R0(размер молекулы). При этом выделитсядополнительная энергия кулоновского взаимодействия Ес. Полная вы-делившаяся энергия и есть энергия связи Есв получившейся молекулы:именно ее надо затратить, чтобы разорвать молекулу на составные ча-сти:

                                                   

Учитывая, что кулоновская энергия , находим отсюда

выражение для равновесного расстояния:

                                              

Применим полученную формулу для оценки размера молекулы КС1.Берем экспериментальные данные: Uт = 4.3 эВ, Uh = 3.8 эВ, Есв =4.8 эВ, так что кулоновская энергия Ес = 4.8 --- 3.8 + 4.3 = 5.3 эВ =5.3 х 1.6 10-19 = 8.5 10-19 Дж. Отсюда легко находим размер молекулы:

                                                    

 

Получившаяся величина примерно в пять раз превышает радиус Бора идает вполне приемлемую оценку размера молекулы.

192

Глава 32. Физическая природа химической связи

Оценим также размер молекулы другого соединения --- НС1, для ко-торого Uт = 13.6 эВ и Есв = 2.7 эВ. Чтобы не повторять аналогичныхвыкладок, используем уже полученный результат. Имеем в этом случае:Ес = 2.7 --- 3.8 +13.6 = 12.5 эВ, что в 12.5/5.3 ? 2.36 больше кулоновскойэнергии для молекулы КСl. Соответственно, размер молекулы будет втакое же число раз меньшим: R0 ?2.7 Е /2.36 = 1.1 Е (эксперимент дает

значение R0= 1,3 Е).

Отчуждение электрона одним ионом у другого (ионная связь) встре-чается в большинстве неорганических соединений, особенно в молекулахиз атомов далеких групп. Кроме соединений щелочных металлов и гало-генов можно привести и другие примеры. Однако изложенные классиче-ские соображения не дают возможности вычислить независимо энергиюсвязи молекулы (или ее размер). Само возникновение равновесного рас-стояния остается вне пределов компетенции такой теории. Силы элек-тростатического притяжения между ионами должны уравновешиватьсяв равновесном состоянии какими-то силами отталкивания. Природа этихсил довольно сложна и связана с перекрытием оболочек ионов. Присближении атомов оболочки начинают сильно деформироваться, что пре-пятствует дальнейшему сближению. Величина R0 --- это равновесноерасстояние между ионами, на котором силы электрического притяже-ния уравновешиваются квантовомеханическим отталкиванием атомов наблизких расстояниях.

Ковалентная связь

 Второй вид связи наблюдается в молекулах, где электроны, осуществля-ющие связь, значительную часть времени проводят в пространстве междуатомами и в какой-то мере являются ``общими"" для обоих ядер. Гомео-полярная (ковалентная) связь характерна для большинства молекул сдвумя одинаковыми атомами (H2, N2, О2 и т.п.). Гомеополярная связь неподдается классическому описанию, а требует квантового рассмотрения.

Рассмотрим простейшую гомеополярную молекулу --- молекулу водо-рода. Впервые это было сделано в 1927 г. Гайтлером и Лондоном. Мыограничимся принципиальным анализом, опуская проведение расчетов,т.к. нашей задачей является уяснение физической природы ковалентной(гомеополярной) связи. Схема взаимодействий в такой молекуле, состоя-щей из двух протонов (ядер атома водорода) А и В и двух электронов 1и 2, показана на рис. 32.1.

32.1. Молекулы

193

 Рис. 32.1: Схема взаимодействий в молекуле водорода.

 Уравнение Шредингера для системы имеет вид:

                                                                                                     

где через  обозначены координаты первого и второго электронов,а H --- гамильтониан системы:

                                                   

                         

                                                           

 

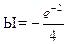
Гамильтониан H1 содержит оператор кинетической энергии электрона1 и потенциальную энергию того же электрона в кулоновском поле ядраА. Аналогичную структуру имеет гамильтониан Я2. Оператор H описы-вает четыре взаимодействия: электрона 1 с ядром В, электрона 2 с ядромА, электронов между собой и ядер --- также между собой. Ядра имеютмассу, примерно в 2000 раз превышающую массу электрона, поэтомуони движутся гораздо медленнее электронов, и в первом приближенииих можно считать неподвижными (такое приближение называется адиа-батическим). Поэтому волновая функция  рассматривается какфункция координат только электронов, а расстояние R между ядрами,важное в проблеме ковалентной связи, входит в волновую функцию Фкак параметр. Получающиеся из уравнения Шредингера собственныезначения энергии будут тогда зависеть от расстояния R, т.е. Е = Е(R),причем в случаях параллельной и антипараллельной ориентации спиновэлектронов характер этой зависимости оказывается различным.

Полная волновая функция зависит не только от пространственных ко-ординат электронов, но и от их спинов. Вследствие принципа Паули

194

Глава 32. Физическая природа химической связи

(согласно которому данный набор квантовых чисел может иметь лишьодна частица), такая полная волновая функция должна быть антисим-метричной относительно перестановки электронов. Поскольку спиновоесостояние не зависит от орбитального, пространственные и спиновые пе-ременные разделяются, и полную волновую функцию электронов в моле-куле водорода можно представить в виде произведения координатной испиновой функций:

                                                                                                     

Из принципа Паули следует, что:

    • если спиновая волновая функция симметрична, тогда пространствен-ная функция антисимметрична;

    • если спиновая волновая функция антисимметрична, тогда простран-ственная функция должна быть симметричной.

 Симметричная спиновая волновая функция соответствует параллель-ному расположению векторов спинов электронов, т.е. суммарному спинуэлектронов S = 1. Такое состояние называется триплетным по числу(2S + 1) = 3 возможных проекций суммарного спина. Во втором жеслучае антисимметричная спиновая функция связана с противоположноориентированными спинами, дающими в сумме 5 = 0, и следовательно,возможно только одно значение проекции полного спина, и состояние на-зывается синг летным.

Взаимодействие между нейтральными атомами, когда расстояние меж-ду ядрами R много больше характерных размеров электронных оболочек(т.е. радиуса Бора аB = 4  

                                                                  

0)2h2) ? ---13.6 эВ. При уменьшении R до нуляэта энергия будет бесконечно возрастать из-за кулоновского отталкива-ния ядер.

Результаты расчетов можно описать следующим образом. Если спиныэлектронов параллельны, то при сближении атомов водорода энергия си-стемы монотонно увеличивается, никакого связанного состояния не воз-никает (кривая Е_ на рис. 32.2). В этом случае предоставленные самимсебе два атома вновь разойдутся, стремясь к состоянию с наименьшейвозможной энергией. Условие существования связанного состояния ---наличие минимума энергии системы при некотором значении Rо --- вы-полняется только при синглетном состоянии электронов, когда их спиныантипараллельны (кривая Е+ на рис. 32.2).

32.1. Молекулы

195

Рис. 32.2: Зависимость энергии Е молекулы водорода от расстояния R между ато-мами. На больших расстояниях имеем два нейтральных атома водорода с общей энергией 2Е0 = 2 ( --- 13.6 эВ) = ---27.2 эВ. Кривая Е_ соответствует триплетномусостоянию электронов и проходит выше асимптотического значения 2Е0 --- связан-ного состояния молекулы в этом случаем не существует. Кривая Е+ соответствуетсинглетному состоянию электронов, она имеет минимум при R = Rо (конечный раз-мер молекулы), расстояние которого от асимптотического значения и есть энергиясвязи Есв молекулы водорода.

 Понять такое поведение энергии можно на качественном уровне, еслирассмотреть два водородных атома, находящихся на большом расстоя-нии 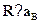 друг от друга. Тогда членом взаимодействия Ы в гамиль-

тониане можно пренебречь, и мы имеем два независимых атома,описываемых суммой гамильтонианов H1иH2. Решения соответствую-щего каждому из них уравнения Шредингера мы уже знаем. Введем обо-значения для получающихся волновых функций: Фа(а) и Фвег)- Тогдарешение для суммы гамильтонианов H1 + H2 будет представляться в видепроизведения волновых функций , а энергия --- в виде суммыэнергий, т.е. будет равна 2Е0 - Физический смысл произведения волновыхфункций очевиден: электрон 1 находится в поле ядра А, а электрон 2 --- вполе ядра В. Но электроны неразличимы, и эта физическая ситуация ни-чем не отличается от случая, когда электрон 2 находится в поле ядра А,а электрон 1 --- в поле ядра В. Этому соответствует иное произведениеволновых функций:, которое тоже является решением урав-нения Шредингера с той же энергией 2Е0 . Согласно принципу суперпо-зиции, решением с этой же энергией будет и любая линейная комбинацияуказанных произведений. Поскольку принцип Паули требует, чтобы пол-

196

Глава 32. Физическая природа химической связи

ная волновая функция была либо симметрична, либо антисимметричнапо пространственным координатам электрона, она должна иметь вид:

                                                                 

где АД --- вычисляемые нормировочные коэффициенты, обеспечивающиеравенство единице полной вероятности:. Подставляясюда выражения и учитывая, что и  уже нормированына единицу, получаем:

                                                                                                             

откуда

                                                 

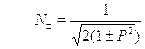
Величина Р, называемая интегралом перекрытия, равна

 P= 

Она характеризует степень перекрытия волновых функций A и B, т.е.степень независимости пространственного распределения электронов другот друга, и играет важную роль в теоретических расчетах свойств мо-лекул.

Если учесть теперь член взаимодействия Ы, то в зависимости от сим-метрии волновой функции Ф получатся поправки к энергии разных зна-ков. В случае антисимметричного состояния _ (полный спин электро-нов S = 1) поправка получается положительной (отталкивание атомов),и связанного состояния не возникает. В случае же симметричного со-стояния + (полный спин электронов S = 0) поправка для больших Rотрицательна (притяжение атомов), что приводит к образованию моле-кулы водорода.

Осмыслить такое поведение поправки к энергии помогает график вол-новой функции. Ось z направим по линии, соединяющей ядра атомов во-дорода, а начало отсчета выберем в средней точке между ядрами, так чтокоординаты ядра А равны , а ядра В . Для про-стоты мы рассмотрим волновые функции на этой оси, причем для случаясимметричного расположения электронов относительно начала отсчета:.,. Тогда

                                          

(32.11)

32.1. Молекулы

197

-5 -4-3-2-1012345

Рис. 32.3: Волновые функции электронов в молекуле водорода на оси, соединяющейядра атомов для синглетного Ф+ и триплетного Ф _ состояний.

 График этих функций представлен на рис. 32.3.

Мы видим, что в обоих случаях существует наибольшая вероятностьнайти электроны вблизи ядер --- волновые функции имеют экстремумыв точках z =R. Однако, при сближении атомов в пространстве междуядрами происходит перераспределение плотности электронов, поведениекоторой различается в зависимости от типа симметрии пространствен-ной части волновой функции --- + или _. В состоянии + электронычасть времени проводят в области между протонами (волновая функ-ция в этой области заметно отлична от нуля). В центре между ато-мами получается электронное облачко, притягивающее к себе протоны--- возникает стягивающее действие и образуется молекула. В состоянииже _ плотность электронов между протонами уменьшается (волноваяфункция проходит через нуль), отталкивание протонов не экранируется,что и приводит к увеличению энергии системы в этом состоянии (см.рис. 32.2). Положение минимума, таким образом, определяется из реше-ния уравнения Шредингера с учетом потенциальной энергии электриче-ского взаимодействия электронов и протонов в молекуле.

Численные результаты R0 = 0,87 Е, Есв = 3.1 эВ для кривой Е+,полученные в таком подходе, следует сравнить с экспериментальными данными: R0 = 0,74 Е, Есв = 4.5 эВ. Разница в энергии связи составляет31%, в размере молекулы --- 17 %.