Федеральное государственное бюджетное учреждение науки
Институт неорганической химии им. А.В. Николаева
Сибирского отделения Российской академии наук
Государственное образовательное учреждение высшего профессионального образования
Новосибирский государственный университет
Факультет естественных наук
Кафедра неорганической химии
Реферат
Волновые функции Хартри, Слэтера, Хартри-Фока. Свойства волновых функций (симметрия, антисимметрия). Волновая функция возбужденных систем, конфигурационное взаимодействие
Преподаватель д.ф.-м.н. Л.Н. Мазалов
Выполнил А.В. Сотников, ФЕН НГУ, группа 090402
Новосибирск 2012
Волновые функции
Одним из основных понятий квантовой механики является волновая функция. Эта функция описывает состояние системы — зная ее, можно определить все физические величины, характеризующие состояние системы. Естественно, имеет смысл говорить лишь о тех характеристиках системы, которые могут быть определены экспериментально при заданных условиях. В квантовой химии рассматривают системы, состоящие из атомных ядер и электронов. Поэтому волновая функция должна зависеть от координат как атомных ядер, так и электронов. Электронная волновая функция описывает состояние электронной системы в атоме или молекуле и зависит от координат электронов.
Волновая функция одноэлектронной системы.Волновую функцию электрона обычно обозначают ψ. Данная функция зависит от координат рассматриваемого электрона: трех пространственных, спиновой, под которой понимают проекцию спина данною электрона на ось z, и от времени. σ -спиновая переменная, которая может принимать два значения: +1/2 и -1/2. Таким образом, одноэлектронная функция записывается как ψ (x, y, z, σ, t). Физический смысл имеет не сама волновая функция, а квадрат ее модуля (в общем случае волновая функция — комплексная величина):
dw = | ψ (x, y, z, σ, t) |2 dv.
В этой записи: dw — вероятность нахождения электрона с проекцией спина σ в момент времени t в элементарном объеме dv, расположенном вблизи точки с координатами (х, у, z). Сам квадрат модуля волновой функции представляет собой плотность вероятности, т. е. вероятность, отнесенную к единице объема. Очевидно, что выбор системы координат (чаще всего используют декартову или сферическую систему координат) не имеет принципиального значения и обусловлен решаемой задачей.
Такая вероятностная трактовка волновой функции имеет ряд следствий. Поскольку вероятность не может быть больше единицы, волновая функция должна принимать лишь конечные значения. Кроме того, волновая функция должна быть однозначной: для электрона не может быть одновременно двух разных вероятностей нахождения в некотором объеме. Наконец, волновая функция должна быть непрерывной (т. е. у функции должна существовать, по крайней мере, первая производная).
Просуммировав вероятности нахождения электрона во всех элементарных объемах, охватывающих все пространство, мы получим вероятность нахождения электрона где-то в пространстве. Если электрон существует, то эта вероятность равна единице:
∫ ψ* (x, y, z, σ) ψ (x, y, z, σ) dτ = 1. (1)
Символ dτ введен здесь для того, чтобы показать, что интегрирование проводится как по пространственным, так и по спиновым переменным. В последнем случае интегрирование фактически заменяется суммированием.
Интеграл в выражении (1) будет иметь конечное значение лишь в том случае, если волновая функция на бесконечности обращается в нуль, что соответствует финитному движению электрона. Для квантовой химии это достаточно очевидное условие, так как электрон в атоме или молекуле находится в ограниченной области пространства вблизи от ядерного остова системы. В случае свободного движения электрона необходимо использовать другие условия нормировки.
Волновая функция многоэлектронной системы. Волновая функция многоэлектронной системы зависит от координат и спинов всех N электронов системы и от времени:
ψ (x1, y1, z1, σ1, x2, y2, z2, σ2, …, xn, yn, zn, σn, t).
В литературе используют сокращенную запись ψ (1, 2, 3, ..., N), в которой под каждым числом подразумевают четыре координаты соответствующего электрона. В случае многоэлектронной системы вероятностная трактовка волновой функции формулируется следующим образом:
d w| ψ (x1, y1, z1, σ1, x2, y2, z2, σ2, …, xn, yn, zn, σn, t) |2 dv1 dv2… dvn.
Величина dw представляет собой вероятность того, что в момент времени t электрон номер 1 с проекцией спина σ1 находится в элементарном объеме dv1, вблизи точки с координатами (x1, y1, z1), электрон номер 2 с проекцией спина σ2 находится в элемент тарном объеме dv2 вблизи точки с координатами (x2, y2, z2),..., а электрон номер n с проекцией спина σn находится в элементарном объеме dvn вблизи точки с координатами (xn, yn, zn). В отличие от случая одноэлектронной системы вероятность нахождения электрона в какой-либо конкретной точке пространства является условной, так как она зависит от того, где в данный момент времени расположены остальные электроны. Говорят, что движение электронов скоррелировано, а связанные с этим эффекты называют корреляционными.
Методы Хартри и Хартри-Фока
Метод Хартри. Полный гамильтониан атома в принятом приближении есть просто сумма одноэлектронных составляющих:
H=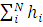 .
.
Энергия атома E является суммой индивидуальных орбитальных энергий εi:
E= ˂ψ| 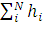 | ψ˃=
| ψ˃=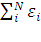
Поскольку электроны считаются независимыми, собственные функции атомного гамильтониана H представляют собой произведение N атомных орбиталей, заселенных электронами,
ψn= ψ1(r1) ψ2(r2)… ψn(rn)
Приближенная многоэлектронная волновая функция такого вида называется волновой функцией Хартри. Теперь перейдем к рассмотрению методу по Хартри.
Достаточно близкие к точным решения уравнения Шредингера получают с помощью метода самосогласованного поля (ССП), предложенного Хартри. В методе ССП межэлектронным отталкиванием не пренебрегают, но действие на данный электрон всех остальных электронов заменяют действием среднего поля, приближенно воспроизводящего их суммарное действие; последнее зависит только от координат рассматриваемого электрона. Это дает возможность разделить в сферической системе координат переменные в уравнении Шредингера.
Полная энергия атома:
E=E’- 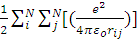 ,
,
А полный гамильтониан принимает вид
H=H’- 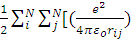 =
= 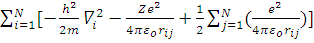
где H’=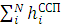 (многоэлектронный гамильтониан).
(многоэлектронный гамильтониан).
Гамильтониан H включает усредненное межэлектронное взаимодействие — системы уравнений Хартри:
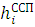 ψi
ψi =
=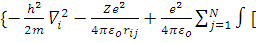 ψj*
ψj*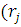 )
)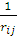 ψj
ψj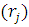 ]drj } ψi
]drj } ψi =εi ψi
=εi ψi , i=1, 2, 3, …, N.
, i=1, 2, 3, …, N.
Каждое такое уравнение зависит от координат лишь одного электрона i, поэтому уравнения Хартри называют одноэлектронными.
Далее задаются некоторым набором N одноэлектронных функций, максимально близких к правильным. С их помощью строят оператор hiссп (0). Затем решают набор одноэлектронных уравнений Хартри, возникающий из условия минимума среднего значения гамильтониана H=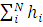 , вычисляемого с волновой функцией Хартри. Полученные решения ψi(1)(ri) используют, чтобы построить «исправленный» оператор hiссп (1), вновь решают ту же систему уравнений, но теперь — с функциями hiссп (1) и т. д. Процесс решения продолжается до тех пор, пока получаемые собственные значения уравнений Хартри будут отличаться от решений, полученных на предыдущей итерации, лишь на малую величину. Этот процесс называется самосогласованием, а результирующее поле, создающее усредненный потенциал, называется самосогласованным полем — отсюда и название метода.
, вычисляемого с волновой функцией Хартри. Полученные решения ψi(1)(ri) используют, чтобы построить «исправленный» оператор hiссп (1), вновь решают ту же систему уравнений, но теперь — с функциями hiссп (1) и т. д. Процесс решения продолжается до тех пор, пока получаемые собственные значения уравнений Хартри будут отличаться от решений, полученных на предыдущей итерации, лишь на малую величину. Этот процесс называется самосогласованием, а результирующее поле, создающее усредненный потенциал, называется самосогласованным полем — отсюда и название метода.
Hn ψn = E ψn
Hn = 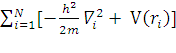
Hno ψn = E ψn-распадается на n-одноэлектронных уравнений:
( ∇21 + V(r1)ψ(r1))=Eψ(r1)
∇21 + V(r1)ψ(r1))=Eψ(r1)
( ∇22 + V(r2)ψ(r2))=Eψ(r2) и т.д.
∇22 + V(r2)ψ(r2))=Eψ(r2) и т.д.
Метод Хартри-Фока. В методе ХФ имеем:
Hn= 
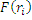 -оператор, который вводится для того, чтобы учесть межэлектронное взаимодействие.
-оператор, который вводится для того, чтобы учесть межэлектронное взаимодействие.
Метод Хартри—Фока является основным расчетным методом квантовой химии. Он представлен в различных вариантах: как для систем с замкнутыми электронными оболочками, так и для систем с открытыми оболочками. Во многих случаях он позволяет получить результаты, достаточные и для интерпретации экспериментальных данных, и для прогнозирования свойств молекулярных систем. Метод позволяет рассчитать полную энергию молекул с точностью до нескольких процентов, что, как правило, недостаточно для расчета относительно малых энергетических эффектов, связанных с химическими превращениями, или электронными возбуждениями в молекулах. Тем не менее, волновая функция метода Хартри — Фока может рассматриваться как очень хорошее начальное приближение для применения более рафинированных подходов. Полученные в ходе решения уравнений Хартри—Фока орбитали используют как стартовые для методов, позволяющих учесть эффекты корреляции, и в рассчетах возбужденных состояний атомов и молекул. Волновая функция многоэлектронной системы выбирается в виде детерминанта Слэтера(о нем мы поговорим ниже). Уравнения Хартри — Фока являют собой одноэлектронные уравнения типа уравнения Шрёдингера, которым соответствуют орбитали , отвечающие минимальным значениям энергии молекулярной системы.
Выражение для полной энергии. Гамильтониан N-электронной системы:
H=
Пробную функцию запишем, в виде одного детерминанта, построенного из N ортонормированных спин-орбиталей:
Ψ(1,2, …, n)=det |ψ1 ψ2 … ψn|
Запишем в развернутом виде выражение для полной энергии молекулы:
E=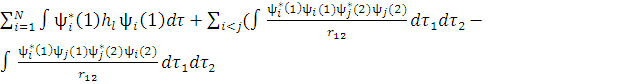 )
)
Численные результаты, получаемые при помощи фундаментального приближения одноэлектронных орбиталей, в основу которого положено предположение о практической независимости движения отдельных электронов, не очень точны. Однако сверх ожидания оказалось, что приближение, развитое в форме метода Хартри — Фока, привело к большим успехам в понимании электронной структуры атомов и молекул. В приближении орбиталей полную волновую функцию N-электронной системы ψ (ξ1, ξ2, …, ξn)выражают приближенно через подобранные орбитальные функции ψ1 (ξ1), ψ2 (ξ2), …, ψn (ξn) где ξ — совокупность пространственных и спиновых координат электрона, а одноэлектронная волновая функция ψi (ξ), называемая также спин-орбиталью, вообще говоря, имеет вид
ψi (ξ)=φiα(r) α(σ)+φiβ(r)β(σ).
Говоря о спин-орбитали, подразумевают комбинированную функцию, объединяющую пространственные орбитали со спиновыми функциями.
Простое произведение спин-орбиталей
П=Пψi(ξi)= ψ1 (ξ1), ψ2 (ξ2), …, ψn (ξn), i=1…N
наиболее ясно выражает идею о размещении электронов по одноэлектронным орбиталям, но само по себе оно не может служить волновой функцией N - электронной системы, так как последняя должна удовлетворять следующим трем требованиям:
1. Быть антисимметричной(свойство антисимметричности волновой функции рассмотрены иже) относительно транспозиции координат ξ i ;, ξ j ,- любой пары электронов (принцип Паули).
2. Являться общей собственной функцией операторов S2, Sz.
3. Иметь трансформационные свойства базиса неприводимого представления точечной группы пространственной симметрии гамильтониана системы.
Детерминант Слэтера
Детерминант Слэтера или слэтеровский детерминант — антисимметричная относительно перестановки частиц волновая функция многочастичной квантовомеханической системы, построенная из одночастичных функций. Детерминант задает простой способ построения антисимметричной функции, необходимой для описания систем, состоящих из многих фермионов. Для этого используется свойство определителя менять знак при перестановке столбцов
ψ =  .
.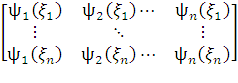 =
=
= det[
det[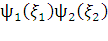 …
… ]
]
Предположим, что входящие функции в этот определитель ортонормированы:
∫ ψi* (ξ) ψj (ξ) dξ = ˂ψi| ψj˃ = δij. (2)
Если это не так, то систему можно ортонормировать с помощью подходящего линейного преобразования, например, методом Шмидта. Убедимся, что такое преобразование не изменяет физического смысла полной волновой функции ψ. С этой целью запишем преобразование Шмидта в матричной форме:
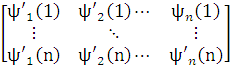 =
=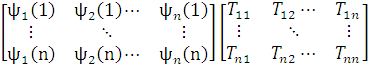
и вспомним, что детерминант произведения АВ двух квадратных матриц А, В равен произведению детерминантов матриц-сомножителей:
det [АВ] = det [A] det [В].
Таким образом,
det{ψ’1(1) ψ’2(2)… ψ’n(n)}= det{ψ1(1) ψ2(2)… ψn(n)}det[T]
Обозначая через ψ’ полную волновую функцию, получаемую в результате преобразования Шмидта,
Ψ’=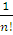 [det{ψ’1(1) ψ’2(2)… ψ’n(n)}]
[det{ψ’1(1) ψ’2(2)… ψ’n(n)}]
находим, что
ψ’= ψdet[T].
Поскольку det [Т] есть просто число, результат применения преобразования к отдельным орбиталям, входящим в состав функции ψ, сводится к перенормировке последней, т. е. не изменяет ее физического смысла. Поэтому можно считать, что совокупность с самого начала ортонормирована условием (2), с учетом которого нормировка полной волновой функции определяется следующим образом:
∫ ψ * ψ dξ1…dξn=˂ ψ | ψ ˃=1/n!
Следовательно, нормированная на единицу полная волновая функция записывается в виде
ψ (ξ1, ξ2, …, ξn) = 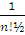 det{ψ1(ξ1) ψ2(ξ2)… ψn(ξn)} = |ψ1(ξ1) ψ2(ξ2)… ψn(ξn)|
det{ψ1(ξ1) ψ2(ξ2)… ψn(ξn)} = |ψ1(ξ1) ψ2(ξ2)… ψn(ξn)|
Обычно ее и называют детерминантом Слэтера. При перестановке двух строк или двух столбцов детерминант Слэтера изменяет знак (функция удовлетворяет принципу Паули).
Конфигурационное взаимодействие
Речь идет о методе расчета, в котором волновая функция молекулы представляется в виде разложения в ряд по детерминантам, описывающим различные электронные конфигурации. Поэтому более корректно было бы говорить не о конфигурационном взаимодействии, а о суперпозиции электронных конфигураций. Метод использует в качестве исходной электронную конфигурацию, отвечающую хартри-фоковскому детерминанту. Можно заменить ее многодетерминантной волновой функцией. В этом случае на уровне в каждом из детерминантов, входящих в волновую функцию, будут одновременно учитываться одно- и двукратные электронные возбуждения. Это позволяет получить весьма точную многоэлектронную волновую функцию, но объем расчетов при этом стремительно возрастает.
Разложение N-электронной волновой функции молекулы по набору однодетерминантных волновых функций, описывающих различные электронные конфигурации, является простым и естественным приемом учета электронной корреляции. Каждая электронная конфигурация отвечает вполне определенному набору орбиталей, и в процессе самосогласованного решения уравнений усредненное по конфигурациям межэлектронное взаимодействие охватывает различные варианты распределения электронов при различных расстояниях (гi - г j) между ними.
В методе конфигурационного взаимодействия (метод CI) многоэлектронная волновая функция раскладывается в ряд по детерминантам Слейтера каждый из которых описывает систему в некотором электронном состоянии. Одно из этих состояний является основным и описывается методами ОХФ или НХФ. Остальные состояния описываются электронными конфигурациями, в которых последовательно учтены возможные переходы электронов с занятых МО на различные незанятые (виртуальные) орбитали. Это означает, что каждый такой детерминант строится из спин-орбиталей, отвечающих основному (ψ о = ψ хф) или одному из возбужденных одноэлекгронных состояний молекулы (ψ к ,k≠0). Соответственно, их классифицируют по числу МО, замещенных виртуальными орбиталями; говорят об одно- двух-, трех-, ..., N-кратно замещенных детерминантах. Занятые и виртуальные МО в методе ХФ ортономированы; соответственно, замещенные детерминанты ортогональны детерминанту основного состояния: ∫ ψo ψk dr =δok . Для систем с открытыми электронными оболочками многоэлектронная волновая функция раскладывается в ряд по линейным комбинациям детерминантов Слейтера, являющимся собственными функциями операторов S и S2 и обеспечивающим чистоту спинового состояния, отвечающего многоэлектронной волновой функции.
Полная волновая KB-функция, учитывающая все возможные электронные конфигурации, имеет вид:
Ψкв=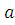 оψо+
оψо+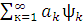
и находится с помощью вариационного принципа. При этом спин-орбитали в каждом слейтеровском детерминанте ψk остаются неизменными (их предварительно рассчитывают методом ХФ), а варьируются только коэффициенты 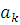 . Среднее значение энергии, вычисленное с волновой функцией, определяется соотношением
. Среднее значение энергии, вычисленное с волновой функцией, определяется соотношением
Eкв= оψо+
оψо+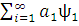 ) |H|(
) |H|(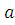 оψо+
оψо+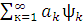 )]=
)]= 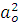 ˂ ψo | H| ψo ˃+[
˂ ψo | H| ψo ˃+[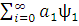 | H|
| H|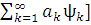 =Eхф+∆E
=Eхф+∆E
Здесь Ехф = 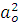 ˂ ψo | H| ψo ˃. Поскольку коэффициент а0 близок к единице, то отрицательная добавка к хартри-фоковской энергии ∆E и есть энергия корреляции Е из выражения для энергии корреляции:
˂ ψo | H| ψo ˃. Поскольку коэффициент а0 близок к единице, то отрицательная добавка к хартри-фоковской энергии ∆E и есть энергия корреляции Е из выражения для энергии корреляции:
Eкор=Eточн-Eхф<0
При бесконечном числе конфигураций (что невозможно) метод КВ обеспечил бы, в принципе, точное решение электронного уравнения Шредингера в пределах базисного набора, который используется для аппроксимации орбиталей. На практике число детерминантов определяется числом электронов в рассматриваемой системе и числом вариантов их размещения на МО; при их полном учете говорят о полном методе КВ. К тому же, число ненулевых матричных элементов точного гамильтониана ˂ψl| H| ψk˃ между конфигурациями ψl и ψk ограничено. Можно строго показать, что матричные элементы точного гамильтониана между основной ψ0 и однократно возбужденной ψ1 электронными конфигурациями равны нулю (теорема Бриллюэна). Кроме того, для детерминантов с тремя и более замещенными по отношению к ψ0, МО матричные элементы ˂ψ0| H| ψk˃ равны нулю (правило Кондона-Слейтера для вычисления матричных элементов). Поэтому даже для приближенной волновой функции только двукратно замещенные детерминанты будут давать существенный вклад в энергию ∆E в выражении для Eкв. Заметим, что однократно замещенные детерминанты будут взаимодействовать с двукратно замещенными, а, следовательно, они тоже повлияют на величину ∆E. Исходя из этого в волновую KB-функцию включают, как правило, однократно и двукратно возбужденные электронные конфигурации, что определяет число детерминантов в многоэлектронной волновой функции
Ψкв=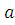 оψо+
оψо+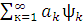 .
.
В то же время для молекул, состоящих более чем из 10 атомов, это позволяет учесть около 90 % корреляционной энергии и понизить тем самым энергию системы на 2—3 эВ; этого, в частности, достаточно, чтобы качественно правильно описать диссоциацию молекулы фтора(приближение CISD).
Следующий уровень повышения точности расчета связан с включением в многоэлектронную волновую функцию трех- (Т) и четырехкратно (Q) замещенных детерминантов; эти методы обозначают как CISDT и CISDTQ соответственно. К сожалению, объем вычислительной работы при этом сильно возрастает, а значит, размер молекул, для которых эти методы применимы на практике, ограничен.
Все «усеченные» варианты метода CI применимы к описанию небольших молекул в электронно-возбужденных состояниях, молекул с открытыми оболочками, диссоциирующих молекул, фотохимических реакций. Однако метод CI не слишком удобен. Сходимость разложения энергии низкая; число однократно замещенных конфигураций пропорционально Мзан x Мсвоб, а двукратно замещенных — пропорционально Мзан 2x Мсвоб2, где Мзан и Мсвоб — число занятых и свободных МО соответственно. Поэтому уже для небольших молекул приходится включать в расчет 106—1012 конфигураций, каждая из которых дает вклад в энергию основного состояния лишь около 10_3 эВ; число подлежащих вычислению матричных элементов гамильтониана между конфигурациями ψ0 и ψk также велико. Кроме этого, расчет «усеченным» методом CI энергии двух молекул, удаленных друг от друга на расстояние нескольких десятков ангстрем, дает результаты, отличные от суммы энергий свободных молекул из-за различий в выборе возбужденных конфигураций фрагментов. Говорят, что нарушается свойство размерной согласованности, присущее методу ХФ и полному методу КВ, когда учитываются все возможные электронные конфигурации. Этот недостаток скорректирован в квадратичном методе КВ (QCISD). Из-за этого расчеты энергии межмолекулярного взаимодействия и энергии диссоциации молекул методом CI недостаточно точны.
Многоконфигурационным методом самосогласованного поля (МК ССП), или multi-configuration self-consistent field (MCSCF), называется вариационный подход, в котором в последовательных циклах самосогласованно оптимизируются как хартри-фоковские МО в детерминантах, так и коэффициенты ак. При этом если оптимизируются все орбитали во всех электронных конфигурациях без ограничения (не считая ограничений, диктуемых симметрией молекулы), метод называется полным МК ССП. Однако можно уменьшить число электронных конфигураций и включить в расчет лишь те из них, которые дают наиболее заметный относительный вклад в энергию. Понятно, что отбор конфигураций может быть сделан различными способами; наиболее популярен ССП-метод полного активного пространства орбиталей (complete active space self- consistent field — CASSCF). В этом методе среди всех МО, формирующих электронные конфигурации, выделяют активные, в качестве которых выступают некоторые высшие занятые и низшие свободные МО, полученные методом ОХФ . Активные МО ищут полным методом КВ с оптимизацией орбиталей. Низколежащие МО, такие как МО атомных остовов, практически не возмущаемые соседними атомами при образовании химической связи и полностью занятые электронами, а также высоколежащие виртуальные МО считаются неактивными; в качестве этих орбиталей используются хартри-фоковские МО. Такой подход не обеспечивает точных абсолютных значений энергии, но хорошо передает относительные изменения энергии из-за изменений в системе, например при диссоциации молекул.
Антисимметричность и симметричность волновой функции
В квантово-химической литературе два возможных значения спина обозначают буквами α и β или символами ↑ и↓: говорят «спин вверх» или «спин вниз», указывая разные значения спина электрона.
Чтобы учесть наличие спина, в аргумент одноэлектронных функций вводят спиновую переменную s, а функцию Ψi(xj)называют спин-орбиталью (xi = ri, si). Пренебрегая малым по сравнению с кулоновским спин-орбитальным взаимодействием, каждую спин-орбиталь Ψi(xi)можно представить в виде произведения пространственной орбитали и спиновой функции σ(si):
Ψi(xi)= Ψi(ri) σ(si)
Важно, что только в нерелятивистской квантовой механике спин вводится так, как это сделано выше. В релятивистской квантовой механике спин является неотъемлемой частью формализма.
Спиновая функция σ(si) является собственной функцией операторов s2 и sz — аналогов операторов квадрата и проекции орбитального момента электрона L2 и Lz соответственно. Для спиновых операторов sk справедливы те же коммутационные соотношения, что и для операторов Lk, к = х, у, z. Кроме того, выполняются следующие соотношения:
S2σ(k) = h2s(s+1)σ(k) =  (
( +1) σ(k), k = α, β;
+1) σ(k), k = α, β;
szσ(k) = mshσ(k), k = α, β; ms = ± ;
;
∫ σ(k) σ(l)dτ=δkl k, l = α, β;
Здесь ms — спиновое магнитное квантовое число. Интегрированием в последнем выражении подразумевается просто суммирование по спинам электрона. Из первого уравнения следует, что
|s| = 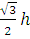
Из-за наличия спина и неразличимости электронов имеются специальные ограничения на вид электронной волновой функции, известные как принцип Паули: электронная волновая функция системы из нескольких электронов должна быть антисимметричной (менять знак) относительно обмена положениями и спинами двух любых электронов i и j:
Ψ(x1, …, xi, …, xj, …)= -ψ(x1, …, xj, …, xi, …).
Отсюда следует, никакие два электрона не могут находиться в одном и том же квантовом состоянии, то есть состоянии, характеризуемом одинаковыми квантовыми числами n, l, m и ms (принцип исключения).
Чтобы понять, как нужно строить волновую функцию с учетом принципа Паули, рассмотрим двухэлектронный атом гелия. Две эквивалентные волновые функции Хартри для основного состояния этой системы имеют вид
Ψ1= ψ1(r1) ψ2(r2)
Ψ2= ψ1(r2) ψ2(r1)
Нижний индекс у аргумента указывает, какой электрон описывает данная орбиталь. Очевидно, что ни одна из функций не является антисимметричной. Однако легко заметить, что связанная с ними функция
Ψ= 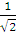 [ψ1(r1) ψ2(r2) - ψ1(r2) ψ2(r1)] (3)
[ψ1(r1) ψ2(r2) - ψ1(r2) ψ2(r1)] (3)
изменит знак при перемене местами аргументов. Если мы попытаемся поместить электроны 1 и 2 на одну и ту же спин-орбиталь ψi в (3), то получим
Ψ= 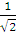 [ψ1(r1) ψ1(r2) - ψ1(r2) ψ1(r1)]
[ψ1(r1) ψ1(r2) - ψ1(r2) ψ1(r1)]
Значит волновая функция вида (3) удовлетворяет принципу исключения Паули.
С математической точки зрения волновая функция (3) есть детерминант из спин-орбиталей
Ψ = 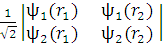
Важным свойством детерминанта является то, что он меняет знак при перестановке двух любых его столбцов или строк; величина детерминанта при этом остается неизменной. Это как раз эквивалентно перемене мест двух электронов: электрон 1 перемещается с орбитали i на орбиталь j, а электрон 2 — с орбитали j на орбиталь i. Если же два столбца или две строки детерминанта одинаковы (что эквивалентно занятию двумя электронами одной и той же орбитали), то детерминант равен нулю.
Итак, принцип Паули диктует, что две спин-орбитали с одинаковыми пространственными частями должны отличаться спиновыми компонентами.
Вернемся к атому Не. Волновая функция основного состояния записывается через определитель следующим образом:
Ψ =  =
= 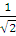 ψ1s(r1) ψ1s(r2)
ψ1s(r1) ψ1s(r2)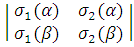 = =
= = 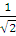 ψ1s(r1) ψ1s(r2)[
ψ1s(r1) ψ1s(r2)[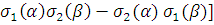
где функция 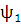
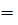
 . Таким образом, функция
. Таким образом, функция 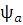 имеет симметричную пространственную часть, тогда как ее спиновая часть, заключенная в квадратные скобки, меняет знак при перемене электронов местами, то есть она антисимметрична. Полный спин системы S = =
имеет симметричную пространственную часть, тогда как ее спиновая часть, заключенная в квадратные скобки, меняет знак при перемене электронов местами, то есть она антисимметрична. Полный спин системы S = =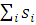 , в основном состоянии равен нулю; такое состояние принято называть синглетным.
, в основном состоянии равен нулю; такое состояние принято называть синглетным.
Нетрудно убедиться, что остальные возбужденные состояния описываются волновыми функциями с антисимметричными пространственными частями и симметричными спиновыми. Полный спин атома в этих случаях равен единице, а состояния называются триплетными, поскольку отвечают трем возможным проекциям спина на ось z: Ms = —1, 0, 1.
Итак, представление многоэлектронной волновой функции в виде детерминанта обеспечивает ее антисимметричные свойства. Какие свойства системы отражает этот факт? Дело в том, что электроны неразличимы, и, следовательно, их перестановка не должна менять свойства системы. Перестановка электронов для волновой функции в виде детерминанта эквивалентна перестановке местами столбцов (строк), что лишь меняет знак детерминанта. Поскольку волновая функция в принципе определена с точностью до фазового множителя, перемена знака свойств системы не меняет.
Детерминант Слейтера является единственной функцией, обеспечивающей антисимметричность волновой функции, записанной через орбитали (орбитальное приближение для волновой функции). Следовательно, он обеспечивает единственность решения соответствующих одноэлектронных уравнений. Понятно, что линейная комбинация детерминантов Слейтера также будет обладать правильными симметрийными свойствами по отношению к перестановке электронов. Это обстоятельство будет использовано нами в дальнейшем, когда мы будем рассматривать волновые функции, выходя за рамки одноэлектронной модели.
Литература
Барановский В.И. Квантовая механика и квантовая химия: учебное пособие для студ. высш. учеб. заведений – М., :Издательский центр «Академия», 2008. - 384 с.
Фудзинага С. Метод молекулярных орбиталей: Пер. с японского – М., : Мир, 1983 -461 с.
Цирельсон В.Г. Квантовая химия. Молекулы, молекулярные системы и твердые тела: учебное пособие для вузов – М., : БИНОМ. Лаборатория знаний, 2012. – 496с.
Степанов Н.Ф. Квантовая механика и квантовая химия. – М., : Мир, 2001. – 519 с.














 (zip - application/zip)
(zip - application/zip)










