Шпоры по математике

1.Матрица. Основные виды матриц.

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.

 Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n — ее порядком

·   . Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю.

Единичной (обозначается е иногда i) называется диагональная матрица с единицами на главной диагонали.

Нулевой называется матрица, все элементы которой равны нулю.

                           2. Матрицы и действия  над ними.  Свойства действий.

Матрицы одинаковых размерностей можно складывать и вычитать. Если

 , , то , причем

, для всех  .

Чтобы умножить матрицу на число, необходимо каждый ее элемент умножить на это число.

Умножение матриц  можно только в том случае, когда число столбцов матрицы  равно числу строк матрицы  в этом случае справедливо соотношение , причем элементы матрицы  равны ,  , . Другими словами строки матрицы  умножаются на столбцы матрицы 

При умножении матрицы справедливы свойства:

1.) - переместительный закон не верен;

2.) ;

3.) ;

4.) ;

5.) ;

6.) .

                      3. Определители матриц. Основные теоремы и свойства определителей

Определителем называется квадратная числовая таблица, вычисляемая по определенным правилам.

Свойства определителей.

1. Определитель не изменится, если его строки заменить столбцами и наоборот, т. Е. .

2. Определитель меняет знак при перестановке любых двух его строк (столбцов).

3. Определитель, имеющий две равные строки (столбца), равен 0.

4. Общий множитель строки (столбца) можно выносить за знак определителя,

5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например

6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число.

7. Определитель треугольной матрицы равен произведению её диагональных элементов.

8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения

9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0.

Правило саррюса для вычисления определителя матрицы 3-тего порядка

 Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус

теорема лапласа

 Пусть ∆ - определитель n-ого порядка. Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

                                    4. Обратная матрица. Теорема об обратной матрице.

Матрица, обозначаемая  , называется обратной к матрице а, если ее произведение с исходной матрицей равно единичной матрице: 

Свойства:

1) 

2) 

3) 

4) 

Теорема о существовании обратной матрицы.

Матрица а имеет обратную  тогда и только тогда, когда определитель отличен от нуля, т.е. Матрица а невырожденная.

                     5. Системы линейных алгебраических уравнений. Решение системы. Совместность.

Под системой линейных алгебраических уравнений (слау) подразумевают систему

Содержащую m уравнений и n неизвестных (x1,x2,…,xn). Прилагательное «линейных» означает, что все неизвестные (их еще называют переменными) входят только в первой степени.

Параметры aij  называют коэффициентами, а bi – свободными членами слау. Иногда, чтобы подчеркнуть количество уравнений и неизвестных, говорят так «m×n система линейных уравнений», – тем самым указывая, что слау содержит m уравнений и n неизвестных.

Решение систем 

Системы можно решить с помощью обратной матрицы и с помощью метода крамера

Совместимость

Теорема кронекера-капелли

·   Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. Ranga=ranga˜.

·   Система называется совместной, если она имеет хоть одно решение. Теорема кронекера-капелли говорит вот о чём: если ranga=ranga˜, то решение есть; если ranga≠ranga˜, то данная слау не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы кронекера-капелли. В формулировке следствия использована буква n, которая равна количеству переменных заданной слау.

                       6. Решение линейных систем  с помощью обратной матрицы и по формулам крамера.

С помощью обратной матрицы

Записать три матрицы: матрицу системы a, матрицу неизвестных x, матрицу свободных членов b.

Найти обратную матрицу a^-1.

Используя равенство x=a^-1⋅b получить решение заданной слау.

С помощью метода крамера

Метод крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

                     7. Ранг матрицы. Способы нахождения ранга. Теорема о ранге матрицы.

Ранг матрицы – это наивысший порядок минора матрицы, отличного от нуля.

Из определения следует, что

·   Для матрицы a размерности m ´ n имеем 0 ≤ rang a ≤ min(m, n);

·   Ранг нулевой матрицы равен нулю;

·   Ранг ненулевой матрицы не меньше единицы;

·   Ранг квадратной матрицы порядка n равен n только тогда, когда ее определитель не равен нулю;

·   Ранг матрицы не меняется при транспонировании.

Теорема если в матрице а имеется минор м порядка r, отличный от нуля, а все миноры матрицы а, окаймляющие минор м (если они существуют) равны нулю, то ранг матрицы а равен r.

Один из методов методом нахождения ранга матрицы является метод перебора миноров. Этот способ основан на определении ранга матрицы.

                                                   8. Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

·   Перестановка местами двух любых её строк (столбцов).

·   Умножение элементов какой-нибудь строки (столбца) на некоторое не нулевое число.

·   Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

                            9. Элементарные преобразования систем линейных уравнений. Метод гаусса.

Метод гаусса

·   Смена мест двух строк;

·   Умножение всех элементов строки на некоторое число, не равное нулю.

·   Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.

·   Вычеркивание строки, все элементы которой равны нулю.

·   Вычеркивание повторяющихся строк.

Элементарные преобразования систем линейных уравнений

1) перестановка любых двух уравнений местами;

2) умножение обеих частей одного уравнения на любое число ;

3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;

10. теорема кронекера – капелли. Примеры.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных

Это соответствует системе: 
-3X₂ + 9X₃ = 6 
-4X₁ + 5X₂ + 7X₃ - 10X₄ = 0 
за базисные переменные примем x₁ и x₂. Тогда свободные x₃,x₄. 
Ранг основной матрицы равен 2. Ранг расширенной матрицы тоже равен 2. Система совместна и имеет бесконечное множество решений.

11.следствия из теоремы кронекера – капелли. Примеры.??????????7

                               12. Однородная система.  Решения однородной системы.

Система линейных уравнений называется однородной, если ее свободные члены равны нулю. Однородная система линейных уравнений всегда совместна, так как нулевой вектор 0 = (0, 0, …, 0) является решением этой системы

Свойства решений однородной системы линейных уравнений

Если вектор а = (a₁, a₂, …, a_n) является решением однородной системы, то вектор k×а = (k×a₁, k×a₂, …, k×a_n) также является решением этой системы, где k – любое число.

Если векторы а = (a₁, a₂, …, a_n) и b = (b₁, b₂, …, b_n) являются решениями однородной системы, то вектор a + b = (a₁ + b₁, a₂ + b₂, …, a_n + b_n) также является решением этой системы.

                                      1. Геометрические векторы, основные определения.

Геометрическим вектором (или просто вектором) называется отрезок, концы которого рассматриваются в определенном порядке

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы– лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

2. Действия над векторами. Свойства действий.

Сложениедвух векторов производится поэлементно, то есть если , то в координатной форме записывается:

 Вычитание двух векторов производится поэлементно, аналогично сложению, то есть если , то в координатной форме записывается

 Умножение вектора на число  покоординатно: 

Свойства

3. Разложение вектора по базису. Базис на плоскости???????

                                            4. Разложение вектора по базису. Базис в пространстве

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n-мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

                         5. Проекция  вектора. Теоремы о проекциях.

Разность x2 − x1 между координатами проекций конца и начала вектора АВ на ось L называется проекцией вектора АБ на эту ось

Т.Проекция вектора a на ось l равна модулю вектора a , умноженному на косинус угла ϕ между вектором и осью:прl a =a cosϕ.

 Т. Проекция суммы двух векторов на ось равна сумме проекций слагаемых векторов на ось.Т. прl (λa)=λпрl a 

                    6. Скалярное произведение векторов. Свойства и приложение

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

теорема косинусов легко выводится с использованием скалярного произведения:

Угол между векторами:

Оценка угла между векторами: в формулезнак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

Проекция вектора на направление, определяемое единичным вектором:,

условие ортогональности[2] (перпендикулярности) векторови:

Площадь параллелограмма, натянутого на два вектораи, равна

Скалярное произведение в координатах

Если то

Угол между векторами

7. Векторное произведение векторов. Свойства и приложение.

Векторным произведением двух векторов a и b будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:

если векторы а и b коллинеарны, он будет нулевым;

он будет перпендикулярен и вектору a​​​​ и вектору b т.е. ∠(ac)=∠(bc)=π2∠ac=∠bc=π2;

его длина определяется по формуле: ∣с∣=∣а∣→∣a∣⋅∣b∣⋅sin∠(a,b) тройка векторов a, b, c имеет такую же ориентацию, что и заданная система координат.

Векторное произведение векторов a и b имеет следующее обозначение: [a×b].

свойства векторного произведения:

1) [a x b]= -[ b x a]

2) [(a1+a2)xb]=[a1 x b]+ [a2 x b]

3) [%*a x b]=%*[ a x b]

8. Смешанное произведение векторов. Свойства и приложение

Смешанным произведением a, b,  и d является та величина, которая равняется скалярному произведению [a×b]×d и  , где [a×b]×b - умножение a и b . Операцию умножения a, b,  и d  зачастую обозначают a⋅b⋅·d→ . Можно преобразовать формулу так: a⋅b⋅d=([a×b],d)

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. 

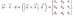
 Объем параллелепипеда, построенного на векторах равен модулю смешанного произведения этих векторов.

2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения

3. Объем треугольной пирамиды равен одной шестой модуля смешанного произведения

4. Векторы планарных тогда и только тогда, когдаВ координатах условие компланарности означает равенство нулю определителя

9. Линии  на плоскости. Виды уравнений  прямой на плоскости.

 Уравнением линии (кривой) на плоскости Oxy называется уравнение, которому удовлетворяют координаты x и y каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии

Уравнение с угловым коэффициентом-

Общее уравнение–, где

Уравнение прямой, проходящей через две заданные точки–

Параметрическое уравнение – 

Каноническое уравнение

Уравнение прямой вотрезках – 

10. Прямая линия на плоскости. Основные задачи (угол между двумя прямыми, деление отрезка и т.д.).

11. Линии в пространстве, уравнения прямой в пространстве.

Общее ур-ие

каноническое

параметрическое

ур-ие леж в 2х точках

угол между прямыми в пространстве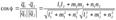

угол между прям и пл

12. Плоскость в пространстве. Виды уравнений плоскости.

Уравнение, имеющее вид  носит название общего уравнения плоскости.

Нормальное уравнение плоскости

Уравнение плоскости в отрезках имеет вид

13. Прямая и плоскость в пространстве. Основные задачи (углы между прямыми, плоскостями, прямой и плоскостью и т.д.).

Уравнение определяет плоскость, проходящую через точкуи имеющую нормальный вектор

– уравнение плоскости в отрезках

. Расстояние d от точки до плоскостиравно

Угол между прямыми

- прямая лежит в плоскости.

- прямая и плоскость пересекаются

Угол между прямой и пл

общее уравнение пл

Угол между плоскостями

                                   14. Эллипс.

Общее уравнение эллипса

Если центр эллипса находится в начале координат и фокусы эллипса находятся на оси на равных расстояниях от начала координат, то уравнение примет вид

Эксцентриситет и коэффициент сжатия эллипсасвязаны соотношением

           15. Гипербола.

Если поместить фокусы гиперболы в точкахто получается каноническое уравнение гиперболы

где Вершинами гиперболы являются точкитогдадействительная ось гиперболы,мнимая ось гиперболы.

Гипербола имеет две асимптоты 

Эксцентриситет гиперболы 

Фокальные радиус-векторы

                                       16. Парабола.

Если директрисой параболы является прямая а фокусом является точкато уравнение параболы имеет вид

Парабола симметрична относительно оси абсцисс 

17. Комплексные числа.

Алгебраическая форма комплексного числа

.

- алгебраическая форма комплексного числа.

комплексные числа  называются комплексно сопряженными

геометрическая интерпретация: комплексно-сопряженные числа  и  отождествляются с точками (х,у) и (х,-у), симметричными относительно оси Ох.

Свойства комплексно-сопряженных чисел:

1. .

2. .

3. .

4. 

                    18. Дробно-рациональная функция. Разложение правильной дроби на простейшие дроби.

Пусть - правильная рациональная дробь,Q(x) – многочлен степени n с коэффициентом перед старшей неизвестной равным единице (для простоты): Q(x)=xⁿ+b₁x^n-1+…+b_n. Q(x) имеет n действительных и комплексных корней. Так как у Q(x) коэффициенты – действительные числа, то комплексные корни попарно сопряжены.

Если Q(x) – многочлен степени n с действительными коэффициентами, то его можно разложить