Приближение Хартри, гамильтониан Хартри

Федеральное государственное бюджетное учреждение науки

Институт неорганической химии им. А.В. Николаева

Сибирского отделения Российской академии наук

Реферат

Приближение Хартри, гамильтониан Хартри, волновая функция по Хартри, полная энергия системы, одноэлектронное уравнение Хартри.

Одинцов Данила Сергеевич

гр. 09402

Проверил:

д. ф.-м. н. Мазалов Лев Николаевич

г. Новосибирск 2012г.

ОДНОЭЛЕКТРОННАЯ МОДЕЛЬ

Метод Хартри - приближенный метод нахождения волновых функций и энергетических состояний квантовой системы со многими электронами. В основе одноэлектронного приближения лежит предположение, что квантовую систему можно описать как систему отдельных электронов, движущихся в усредненном потенциальном поле, которое учитывает взаимодействие как с ядрами атомов, так и с другими электронами. Волновая функция многоэлектронных системы в одноэлектронном приближении выбирается в виде детерминанта Слейтера определенного набора функций, зависящих от координат одной частицы. Эти функции являются собственными функциями одноэлектронного гамильтониана с усредненным потенциалом.

Рассмотрим, как с помощью вариационного принципа можно найти волновые функции и уровни энергии неподвижного Н-электронного атома, максимально близкие к точным. Напомним, что волновая функция такого атома зависит от энергии межэлектронного взаимодействия, то есть требует учета мгновенных положений всех электронов, что является причиной затруднений при решении уравнения Шредингера.

H=T_Э(r) + V_эя(r) + V_ээ(r)= −ћ/2m−+ i<j (1)

 Поэтому вначале просто исключим из гамильтониана оператор энергии межэлектронного взаимодействия V_ээ.  В этом случае многоэлектронное уравнение Шредингера распадается на систему N одноэлектронных, то есть зависящих от координат только одного электрона, уравнений:

h_iχ_i(r_i)=i= 1,2,3...N  (2)

 В каждом из одноэлектронных гамильтонианов

 h_i=(ћ²/2m)*–(Ze²/4π) (3)

 первый член описывает кинетическую энергию электрона в i-м состоянии, а второй- потенциальную энергию его притяжения к ядру, тогда как Е; есть энергия электрона в i-м состоянии. В принятом приближении поведение каждого i-го электрона не зависит от поведения остальных электронов и описывается некоторой волновой функцией  подобно единственному электрону в атоме водорода. В этом состоит суть приближения независимых частиц, которое носит довольно общий характер и используется в различных квантово-механических задачах.  Применительно к многоэлектронным атомам оно известно как одноэлектронная модель. Решения   одноэлектронных уравнений (2) называются одноэлектронными волновыми функциями, или орбиталями. В атоме они носят название атомных орбиталей, в молекуле - молекулярных, в кристалле - кристаллических;  энергии есть энергии соответствующих одноэлектронных состояний. Такой подход называют также орбитальным приближением. Полный гамильтониан атома в принятом приближении есть просто сумма одноэлектронных составляющих  H=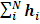(4) i а энергия атома Е является суммой индивидуальных орбитальных энергий

 E= (5)

Поскольку электроны считаются независимыми, собственные функции атомного гамильтониана Н представляют собой произведение N атомных орбиталей, заселенных электронами

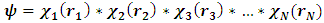  (6)

 Приближенная многоэлектронная волновая функция вида (2.30) называется волновой функцией Хартри. Соответствующая функция распределения электронов в пространстве имеет вид

 |²=

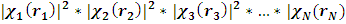 |²      (7)

Структура функции распределения Хартри (7) такова, что вероятность найти i-й электрон в элементе объема dr_i вблизи точки r_i равна,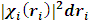   независимо от того, где находятся остальные (N- 1) электронов.

Гамильтониан (4) является, конечно, чрезмерно упрощенным. Во-первых, энергия межэлектронного отталкивания не мала, и пренебрегать ею нельзя. Во-вторых, эта энергия зависит от расстояний между парами всех электронов, причем, при изменении положения любого из электронов согласованно меняются расстояния, а значит и взаимодействия между всеми остальными электронами. Говорят, что существует корреляция в движении электронов, и для многоэлектронных систем учет этой корреляции является сложной и часто необходимой задачей. Например, игнорируя корреляцию, невозможно получить правильные оценки энергии диссоциации молекул, а следовательно и понять механизм этого явления.

МЕТОД САМОСОГЛАСОВАННОГО ПОЛЯ

САМОСОГЛАСОВАННОЕПОЛЕ в квантовой механике - эффективное  силовое поле, создаваемое частицами сложной системы (атома, атомного ядра, твёрдого тела и др.). Служит для приближённого описания взаимодействия между частицами путём его замены воздействием самосогласованного поля на каждую из них; при этом решение много частичной задачи сводится к рассмотрению движения отдельной частицы в самосогласованном поле (и во внеш. поле, если оно имеется). Имея сходную с последним структуру, самосогласованное поле отличается тем, что зависит от состояния системы, определяемого самим же Самосогласованным полем Это требует согласования вида самосогласованного поля с решениями динамических уравнений, зависящими в свою очередь от самосогласованного поля, с чем и связан термин «самосогласованное».

Самосогласованное поле описывает лишь часть взаимодействия между частицами, отвечающую воздействию среднего распределения частиц системы на каждую из них. За рамками метода самосогласованного поля остаётся корреляционная (флуктуационная) часть взаимодействия, связанная с отличием мгновенного распределения частиц от среднего. Во многих случаях корреляции играют незначительную роль, и применение метода самосогласованного поля оправдано. Однако в ряде явлений эта роль является определяющей.

Достаточно близкие к точным, решения уравнения Шредингера получают с помощью метода самосогласованного поля (ССП), предложенного Хартри. В методе сел межэлектронным отталкиванием не пренебрегают, но действие на данный электрон всех остальных электронов заменяют действием среднего поля, приближенно воспроизводящего их суммарное действие; последнее зависит только от координат рассматриваемого электрона. Это дает возможность разделить в сферической системе координат переменные в уравнении Шредингера. С формальной точки зрения это достигается следующим образом. Одноэлектронный гамильтониан записывают в виде

 (ћ²/2m)* – (Ze²/4π)+ i=1,2,3...N(i) (8)

Каждый из членов, входящих в слагаемое  описывает отталкивание между электронами i и j, усредненное по всем положениям электрона j, и, следовательно, зависящее только от координат электрона i. Таким образом, их сумма описывает среднее взаимодействие электрона i с остальными (N- 1) электронами. Последствия этого приближения состоят в следующем. Рассмотрим многоэлектронный гамильтониан  (9) Его собственные функции (функции Хартри) имеют вид орбитальных произведений (6), а среднее значение  представляется суммой собственных значений

h_i^ccп:  (10)

Последнее выражение напоминает соотношение (5), однако смысл энергий Е_i в (10) иной: теперь Е_i есть сумма кинетической энергии i-го электрона, потенциальной энергии его притяжения к ядру и средней потенциальной энергии его отталкивания от остальных (N- 1) электронов. Следовательно, энергия Е" есть сумма кинетической энергии всех электронов, потенциальной энергии их притяжения к ядру и удвоенной потенциальной энергии их усредненного отталкивания от остальных электронов. Удвоение возникло потому, что отталкивание между электронами i и j учтено в (9) дважды: как среднее по j в h_i^ccп и среднее по i в h_i^ccп  (8). С учетом сказанного полная энергия атома равна

-  (11)

а полный гамильтониан атома принимает вид  

H=ℋ-           (12)

Таким образом, мы свели задачу решения уравнения Шредингера для многоэлектронного атома к решению системы N уравнений с гамильтонианом (2.36), включающим усредненное межэлектронное взаимодействие системы уравнений Xapтри:

={-}χ_i(r_i)=i=1,2,3,...,N  

 (13)

Каждое уравнение (13) зависит от координат лишь одного электрона i, поэтому уравнения Хартри называют одноэлектронными. Чтобы решить эту систему уравнений, нужно построить набор операторов h_i^ccп, для чего следует прежде рассчитать усредненные величины˂(e²/4πE₀r_ij)˃. Вероятность того, что j-й электрон с волновой функцией χ_ij(r_j) находится в бесконечно малом объеме dr_j равна χ_j²dr_j (рис. 1.).

Рисунок 1 Иллюстрация к вычислению усредненного электронно-кулоновского взаимодействия

Значит, энергия отталкивания i-го электрона, усредненная по всем положениям j-ro электрона, равна Однако, чтобы вычислить этот интеграл, волновые функции χ_j(r_j) должны уже быть известны и мы как раз хотим их найти из  уравнений (13). Это противоречие преодолевается следующим образом. Сначала задаются некоторым набором N одноэлектронных функций, максимально близких к правильным  χ_j⁽⁰⁾(r_j);позже мы увидим, что сделать это нетрудно. С их помощью вычисляют интеграл (14) и строят оператор h_i^ccп(0) (8). Затем решают набор одноэлектронных уравнений Хартри, возникающий из условия действия минимума среднего значения гамильтониана (4), вычисляемого с волновой функцией Хартри (6). Полученные решения χ_i⁽¹⁾(r_i) используют, чтобы построить <<исправленный>> оператор h_i^ccп(1), вновь решают ту же систему уравнений, но теперь - с функциями h_i^ccп(1) и т. д. Процесс решения продолжается до тех пор, пока получаемые собственные значения уравнений Хартри будут отличаться от решений, полученных на предыдущей итерации, лишь на малую величину -10-6 ат. ед. Этот процесс называется самосогласованием, а результирующее поле, создающее усредненный потенциал в (8), называется самосогласованным полем отсюда и название метода. Отметим, что сходимость метода не гарантируется теорией, но, как правило, достигается на практике. Существуют довольно хорошо разработанные процедуры, которые позволяют обойти встречающиеся здесь иногда затруднения, такие, например, как отличие симметрии усредненного потенциала от действительной симметрии системы. Вернемся к физическому содержанию многоэлектронной волновой функции Хартри (6) и соответствующей функции распределения электронов (7). Их вид таков, как будто поведение каждого из электронов не зависит от остальных электронов. Теперь мы видим, что это не так: орбитали χ_j(r_j) определяются самосогласованно; это означает, что поведение каждого из электронов зависит от поведения остальных, хотя взаимное влияние электронов в методе ССП учитывается не прямо, а опосредованно, через усредненный потенциал (14). Конечно, часть информации при этом теряется. Одноэлектронное приближение и метод ССП на первый взгляд кажутся довольно грубыми, однако, это не так. Дело в том, что быстродвижущийся электрон чувствует скорее среднее эффективное поле остальных частиц, чем реагирует на мгновенные изменения их позиций. Принципиально важно, что самосогласованные решения удовлетворяют вариационному принципу, то есть приводят к средним значениям энергии состояний, которые являются оценками сверху для точных энергий.

Список использованной литературы:

1)      Цирельсон В.Г. Ц86 Квантовая химия. Молекулы, молекулярные системы и твердые тела: учебное пособие для вузов/ -М.: БИНОМ. Лаборатория знаний, 2010. С 90- 95. ISBN 978-5—9963-0080-8

2)      Энциклопедия физики и техники: http://www.femto.com.ua// самосогласованное поле