Дифференциальные уравнения гиперболического типа

Курсовая работа студента гр. МТ-31 Нургалиев А.

Инновационный евразийский университет

Павлодар 2007 год.

1. Введение.

Многие задачи математической физике приводят к дифференциальным уравнениям с частными производными. В настоящей курсовой работе рассмотрены одни из основных уравнений гиперболического типа: 4-го и наиболее часто встречающегося 2-го порядка.

Рассмотрено простейшее уравнение гиперболического типа – волновое уравнение. К исследованию этого уравнения приводят рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т. д. Приведена формула Даламбера для решения краевых задач, а также её физическая интерпретация.

Большое число задач о колебаниях стержней, пластин и т.д. приводит к уравнениям более высокого порядка. В качестве примера на уравнения 4-го порядка рассмотрена задача о собственных колебаниях камертона.

2. Метод распространяющихся волн.

2.1. Вывод уравнения колебаний струны.

В математической физике под струной понимают гибкую, упругую нить. Напряжения, возникающие в струне в любой момент времени направлены по касательной к ее профилю. Пусть струна длины l в начальный момент направлена по отрезку оси 0x от 0 до l. Предположим, что концы струны закреплены в точках x=0 и x=l. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя струны, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения – говорят, струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.

Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси 0x и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией u(x,t) которая дает величину перемещения точки струны с абсциссой x в момент t.

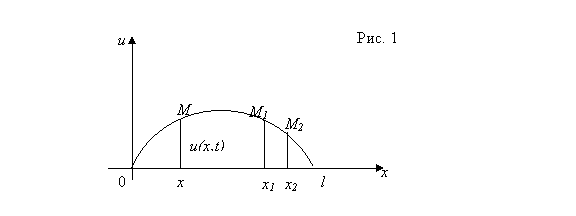
Так как мы рассматриваем малые отклонения точек струны в плоскости (x,u), то будем предполагать, что длина элемента струны M1M2 равняется ее проекции на ось 0x, т.е. M1M2=x2-x1. Также будем предполагать, что натяжение во всех точках струны одинаковое; обозначим его через T.

Рассмотрим элемент струны MM^.

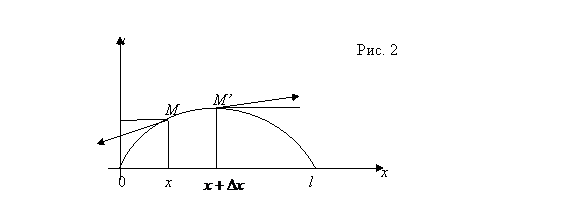
На концах этого элемента, по касательным к струне, действуют силы T. Пусть касательные образуют осью 0x углы  и . Тогда проекция на ось 0u сил, действующих на элемент MM^, будет равна . Так как угол  мал, то можно положить , и мы будем иметь:

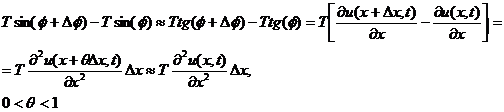
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).

Чтобы получить уравнение движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции. Пусть масса элемента струны будет . Ускорение элемента равно . Следовательно, по принципу Даламбера будем иметь:

Сокращая на  и обозначая , получаем уравнение движения

 (1)

Это и есть волновое уравнение – уравнение колебания струны. Для полного определения движения струны одного уравнения (1) недостаточно. Искомая функция u(x,t) должна удовлетворять еще граничным условия, указывающим, что делается на концах струны (x=0 и x=l), и начальным условиям, описывающим состояние струны в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями:

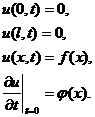
2.2. Формула Даламбера.

Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с задачи с начальными условиями для неограниченной струны:

 (2)

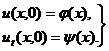 (3)

Преобразуем это уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик

распадается на два уравнения:

, ,

интегралами которых являются прямые

, .

Вводя новые переменные

, ,

уравнение колебания струны преобразуем к виду:

. (4)

Найдем общий интеграл последнего уравнения. Очевидно, для всякого решения уравнения (4)

,

где  - некоторая функция только переменного . Интегрируя это равенство по  при фиксированном , получим

, (5)

где  и  являются функциями только переменных  и .Обратно, каковы бы ни были дважды дифференцируемые функции  и , функция , определяемая формулой (5), представляет собой решение уравнения (4). Так как всякое решение уравнения (4)может быть представлено в виде (5) при соответствующем выборе  и , то формула (5) является общим интегралом этого уравнения. Следовательно, функция

 (6)

является общим интегралом уравнения (2).

Допустим, что решение рассматриваемой задачи существует; тогда оно дается формулой (6). Определим функции  и  таким образом, чтобы удовлетворялись начальные условия:

 (7)

. (8)

Интегрируя второе равенство, получим:

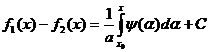
где  и C – постоянные. Из равенства

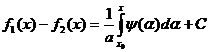
находим:

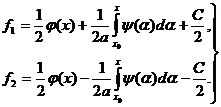 (9)

Таким образом, мы определили функции  и  через заданные функции  и , причем равенства (9) должны иметь место для любого значения аргумента. Подставляя в (6) найденные значения  и , получим:

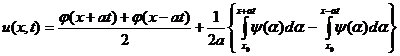
или

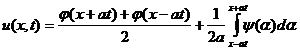, (10)

Формулу (10), называемую формулой Даламбера, мы получили, предполагая существование решения поставленной задачи. Эта формула доказывает единственность решения. В самом деле, если бы существовало второе решение задачи (2) – (3), то оно представлялось бы формулой (10) и совпадало бы с первым решением.

Нетрудно проверить, что формула (10) удовлетворяет (в предположении двукратной дифференцируемости функции  и однократной дифференцируемости функции ) уравнению и начальным условиям. Таким образом, изложенный метод доказывает как единственность, так и существование решения поставленной задачи.

2.2.2.Физический интерпретация.

Функция , определяемая формулой (10), представляет собой процесс распространения начального отклонения и начальной скорости. Если фиксировать , то функция  дает профиль струны в момент , фиксируя , получим функцию , дающую процесс движения точки . Предположим, что наблюдатель, находившийся в точке x=0 в момент t=0, движется со скоростью a в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая , . В этой подвижной системе координат функция  будет определятся формулой  и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция  представляет неизменный профиль f(x), перемещающийся вправо (в положительном направлении оси x) со скоростью a (распространяющуюся или бегущую волну). Функция f(x+at) представляет, очевидно, волну, распространяющуюся налево (в отрицательном направлении оси x) со скоростью a. Таким образом, общее решение (10) задачи Коши для бесконечной струны есть суперпозиция двух волн , одна из которых распространяется направо со скоростью a, а вторая – налево с той же скоростью. При этом

,

где .

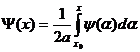Для выяснения характера решения (10) удобно пользоваться плоскостью состояний (x,t) или «фазовой плоскостью». Прямые x-at=const и x+at=const являются характеристиками уравнения (2). Функция  вдоль характеристики x-at=const сохраняет постоянное значение, функция  постоянна вдоль характеристики x+at=const.

Предположим, что f(x) отлична от нуля только в интервале  и равна нулю вне этого интервала. Проведем характеристики  и  через точки  и ; они разбивают полуплоскость (x,t>0) на три области I, II, и III (рис. 3, а).

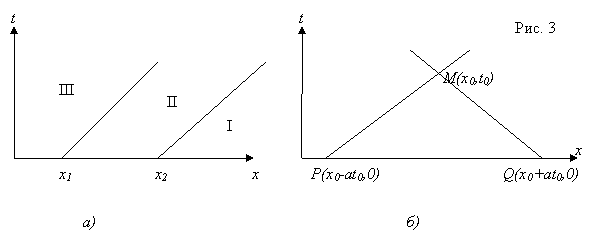
Функция  отлична от нуля только в области II, где  и характеристики  и  представляют передний и задний фронты распространяющейся направо волны.

Рассмотрим теперь некоторую фиксированную точку  и приведем из нее обе характеристики  и , которые пересекут ось x в точках , t=0 и , t=0. Значение функции  в точке  равно , т. е. определяется значениями функций и  в точках  и , являющихся вершинами треугольника MPQ (рис. 3, б), образованного двумя характеристиками и осью x. Этот треугольник называется характеристическим треугольником точки . Из формулы (10) видно, что отклонение  точки струны в момент  зависит только от значений начального отклонения в вершинах P(x0-at0,0) и Q(x0+at0,0) характеристического треугольника MPQ и от значений начальной скорости на стороне PQ. Это становится особенно ясным, если формулу (10) записать в виде

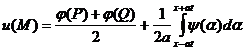 (11)

Начальные данные, заданные вне PQ, не оказывают влияния на значения  в точке . Если начальные условия заданы не на всей бесконечной прямой, а на отрезке , то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок .

2.2.3. Пример.

Решение (10) можно представить в виде суммы , где

 (12)

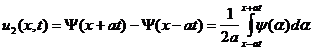. (13)

Если начальная скорость равна нулю (), то отклонение  есть сумма левой и правой бегущих волн, причем начальная форма обеих волн определяется функцией , равной половине начального отклонения. Если же , то  представляет возмущение струны, создаваемое начальной скоростью.

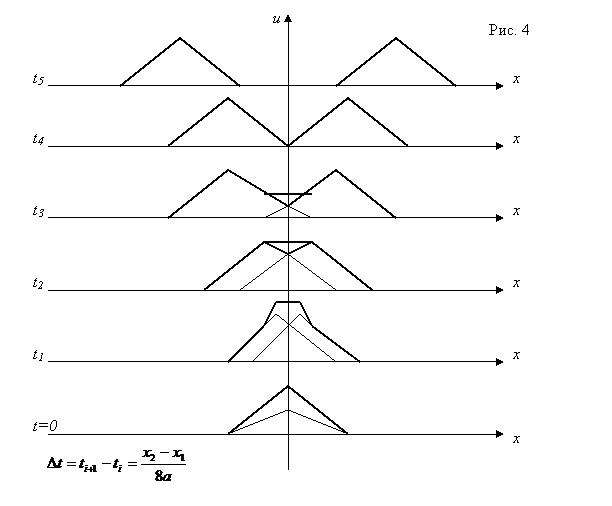
Рассмотрим распространение начального отклонения, заданного в виде равнобедренного треугольника. Такой начальный профиль можно получить, если оттянуть струну в середине отрезка  . На рис. 4 даны последовательные положения струны через промежутки времени .

Наглядное представление о характере процесса распространения можно получить с помощью фазовой плоскости (x, t). Проведем характеристики через точки  и ; они разобьют полуплоскость  на шесть областей (рис. 5).

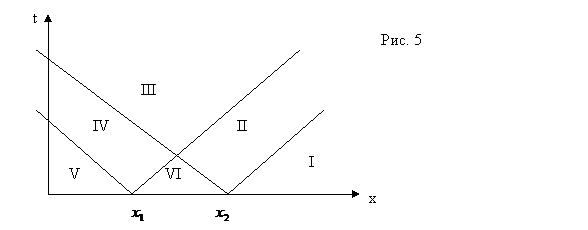
Отклонение  в любой точке (x,t) дается формулой (12). Поэтому в областях I, III, V отклонение равно нулю, так как характеристический треугольник любой точки из этих областей не имеет общих точек с отрезком , на котором заданы начальные условия. В области II решением является «правая волна» , в области IV – «левая волна» , а в области VI решение есть сумма «левой» и «правой» волн.

3. О колебании стержней.

В курсах методов математической физики основное место отводится уравнениям второго порядка. Однако большое число задач о колебаниях стержней, пластин и т.д. приводит к уравнениям более высокого порядка.

В качестве примера на уравнения 4-го порядка рассмотрим задачу о собственных колебаниях камертона, эквивалентную задаче о колебаниях тонкого прямоугольного стержня, зажатого одним концом в массивные тиски. Определение формы колебаний камертона и его частоты сводится к решению «уравнения поперечных колебаний стержня»

 (1)

К этому уравнению приходят во многих задачах о колебании стержней, при расчете устойчивости вращающихся валов, а также при изучении вибрации кораблей.

Приведем элементарный вывод уравнения (1). Рассмотрим прямоуголный стержень длиной , высотой h и шириной b. Выделим элемент длины dx. После изгиба торцевые сечения выделенного элемента стержня, предполагаемые плоскими, образуют угол , Если деформации малы, а длина оси стержня при изгибе не меняется (dl=dx), то

.

Слой материала, отстоящий от оси стержня y=0 на расстоянии , изменяет свою длину на величину . По закону Гука сила натяжения, действующая вдоль слоя, равна

,

где E – модуль упругости материала стержня. Полный изгибающий момент сил, действующих на сечение x, равен

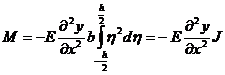, (2)

где

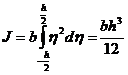
- момент инерции прямоугольного сечения относительно своей горизонтальной оси. Обозначим через M(x) момент, действующих на правую часть стержня в каждом сечении. В сечении x+dx, очевидно, действует момент сил, равный –(M+dM).

Избыточный момент –dM уравновешивается моментом тангенциальных сил

.

Отсюда в силу равенства (2) получаем величину тангенциальной силы

. (3)

Приравняв действующую на элемент результирующую силу

произведению массы элемента на ускорение

,

где  - плотность стержня, S – площадь поперечного сечения (при этом мы пренебрегаем вращательным движением при изгибе), получаем уравнение поперечных колебаний стержня

 (). (1)

Граничными условиями для заделанного конца x=0 являются неподвижность стержня и горизонтальность касательной

, . (4)

На свободном конце должны равняться нулю изгибающий момент (2) и тангенциальная сила (3), откуда следует, что

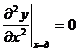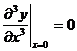, . (5)

Для того чтобы полностью определить движения стержня, нужно еще задать начальные условия – начальное отклонение и начальную скорость

,  (). (6)

Таким образом, задача сводится к решению уравнения (1) с граничными условиями (4), (5) и с начальными условиями (6).

Будем решать задачу методом разделения переменных, полагая

y=Y(x)T(t). (7)

Подставляя предлагаемую форму решения в (1), имеем:

.

Для функции Y(x) получаем задачу о собственных значениях

, (8)

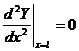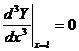, , , . (9)

Общее решение уравнения (8) представляется в виде

.

Из условий Y(0)=0, Y^(0)=0 находим C=-A, D=-B. Отсюда следует, что

.

Условия Y^^(l)=0 и Y^^^(l)=0 дают:

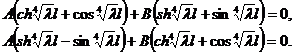
Эта однородная система имеет нетривиальные решения A и B, если определитель системы равен нулю. Приравнивая этот определитель нулю, получаем трансцендентное уравнение для вычисления собственных значений

.

Так как , то это уравнение можно записать в идее

 (). (10)

Корни уравнения (10) без труда вычисляются, например, графически

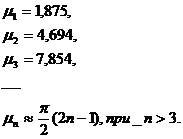
Последняя формула дает значение  с точностью до трех десятичных знаков, начиная с n=3, и с точностью до шестого знака для .

Рассмотрим теперь частоты колебаний камертона. Уравнению

Удовлетворяют тригонометрические функции

с частотой

,

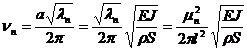Частоты  собственных колебаний относятся как квадраты . Так как

,

То второй собственный тон выше основного тона более чем на две с половиной октавы, т.е. выше шестой гармоники струны при равном основном тоне, третье же собственное колебание выше основного тона более чем на четыре октавы. Например, если камертон имеет основную частоту в 440 колебаний в секунду (принятый стандарт a^ – ноты ля первой октавы), то следующая собственная частота камертона будет 2757,5 колебания в секунду (между c^^^^ =2637,3 и f^^^^=2794,0 – между нотами ми и фа четвертой октавы равномерно-темперированной гаммы), третья же собственная частота в 7721,1 колебания в секунду уже выходит за пределы шкалы собственно музыкальных звуков.

При возбуждении колебаний камертона ударом присутствует не только первая, но и высшие гармоники, чем и объясняется металлический звук в начальный момент. Однако с течением времени высшие гармоники быстро затухают и камертон издает чистый звук основного тона.

4. Заключение.

Дифференциальные уравнения с частными производными широко применяются в математической физике. В качестве примера в данной работе рассмотрены два уравнения.

Волновое уравнение с краевыми условиями можно свести к решению формулы Даламбера, задающуюся начальными условиями. И с помощью фазовой плоскости можно отследить характер его решения.

В процессе решения «уравнения поперечных колебаний стержня» получаем задачу о собственных значениях и задачу о нахождение частот собственных колебаний. Причем частоты собственных колебаний относятся как квадраты собственных значений.

Список литературы

А. Н. Тихонов, А. А. Самарский «Уравнения математической физики», Москва, 1966 г.

Н. С. Пискунов «Дифференциальное и интегральное исчисление», Москва, 1970 г.

Н. С. Кошляков, Э. Б. Глинер, М. М. Смирнов «Уравнения в честных производных математической физики», Москва, 1970 г.